Иллюстрированный самоучитель по Mathematica 5

Нахождение решений дифференциальных уравнений

Решает дифференциальные уравнения функция DSolve.

Пример 10.4.
Решим уравнение у'''+4у' = sec 2t.

Решение. Конечно, это линейное дифференциальное уравнение третьего порядка. Поэтому его решение содержит три произвольные постоянные и является суммой какого-нибудь решения неоднородного уравнения и общего решения соответствующего однородного уравнения. Однако система Mathematica знает все это и без нас и выдает решение сразу.

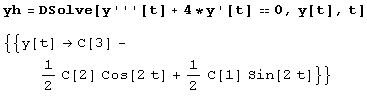
Как видите, система Mathematica обозначает произвольные постоянные через С[1],С[2],С[3] и т. д.

Пример 10.5.
Решим уравнение 4у'² -9х = 0.

Решение.

Yh=DSolve[4y'[х]^2-9х == 0,у[х], х]
{{у[х] › -х^3/2 +С[1]},{у[х] › х^3/2 +С[1]}}.

Заметьте, что в учебниках и задачниках это решение обычно записывается в неявной форме: (у-C)² = х³.

Пример 10.6.
Решим уравнение х = y'+sin у'.

Решение.

Как видим, в данном случае функция DSolve с поиском решения не справилась. Тем не менее решение может быть представлено в параметрической форме: х = p+sin р, у = p² /2+psin p+cos р+С.

Впрочем, не спешите обвинять функцию DSolve – ведь решение записано нами не в виде явной функции!

Вот еще один пример, когда решение находится как неявная функция.