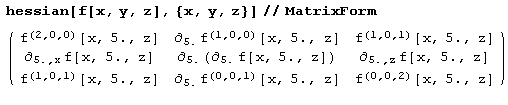Векторный анализ
Операции векторного анализа легко определить самостоятельно. Для этого полезны функции Outer и Inner. Функция Outer позволяет создать декартово произведение двух списков. Вот как можно, например, создать список пар, первый элемент которых берется из первого списка, а второй – из второго.
Outer[List,{a,b,c}, {d, e, f} ] {{{a,d}, {a,e},{a,fn,{{b,d},{b,e},{b,f}},{{c,cl},{c,e},{c,f}}}Вот пример, связанный с конкатенацией строк.

Вот числовой пример.
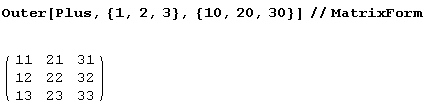
Функция Inner немного похожа на скалярное произведение. Собственно говоря, inner[f, список1, список2, g] и есть скалярное произведение, в котором умножение замещается функцией /, а сложение – функцией g.
vl = {a1, a2, a3}; v2 = {b1, b2, b3}; Dot[vl,v2] a1 b1 + 32 b2 + a3 b3 Inner[Times,vl,v2,Plus] a1 b1 + 32 b2 + a3 b3Теперь можем определить основные операции векторного анализа.
Вот определение градиента.
gradient[f,x_List] := Map[D[f,#]&,x]Вычислим градиент.
Gradient[f[x,у, z], {x,y,z}]
{f(0.1.0) [x, y, z], f(0.1.0) [x, y, z],
f(0.1.0) D[x, y, z]}.
Теперь определим гессиан:
hessian[f_,x_List] := Outer[D,gradient[f,x],x]И вычислим его: