Векторный анализ
Систему координат и название переменных можно изменить.
SetCoordinates[Cartesian[x,y,z]] Cartesian[x,y,z]Мы установили декартову систему координат, но изменили название переменных. Посчитаем дивергенцию.
Div[{x y,x y z,Sin[x y z]}] y+x z+x y Cos[x y z]Установим теперь сферическую систему координат.
SetCoordinates[Spherical[r,th,ph]] Spherical[r,th,ph]Узнаем промежутки изменения координат.
CoordinateRanges[] (0<r<∞, 0<th<π, - π<ph<π}Напишем формулы преобразования координат.
CoordinatesToCartesian[[r,th,ph)] {r Cos[ph] Sin[th],r Sin[ph] Sin[th],r Cos[th]}Найдем якобиан.
Jdet=JacobianDeterminant[ ]
r2 Sin [th].
Шутки ради вычислим площадь поверхности сферы радиуса R:
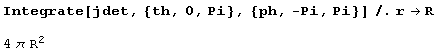
И объем сферы радиуса R:
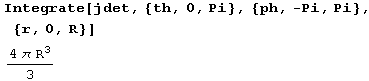
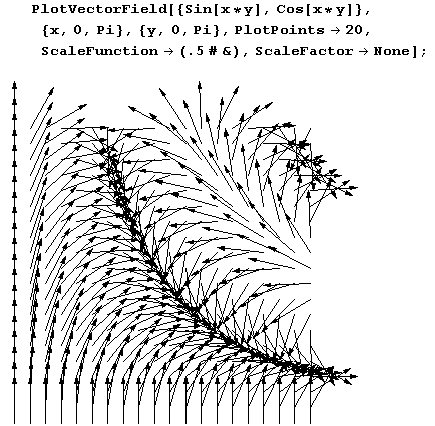
При решении многих задач весьма полезно изображать векторные поля графически. Для изображения двухмерных полей следует подгрузить пакет:
<<Graphics `PlotField`Вот как с его помощью можно изобразить двухмерное поле.