Векторный анализ
Определяем теперь лапласиан:
laplacian[f_,x_List] := Inner[D,gradient[f,x],x]И вычисляем его:
Laplacian[f[x,y,z], {x,y,z}]
f(0.0.2) [x, y, z] + f(0.2.0) [x, y, z] f(2.0.0) [x, y, z].
Совсем несложно определить и якобиан.
jacobian[f_List,x_List] := Outer[D,f,x]Вот пример его вычисления.
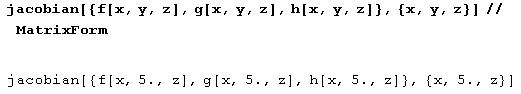
Наконец, определяем дивергенцию.
divergence[f_List,x_List] := Inner[D,f,x]Вот пример ее вычисления.
Divergence [ {f [x, у, z], g [x, у, z], h [x, y, z] }, {x, y, z} ]
h(0.1.0) [x, y, z] +
g(0.0.1) [x, y, z]+f(1.0.0) [x, y, z].
Вот еще несколько примеров выполнения операций векторного анализа.
f=x^2+x y^2+x y z^2;g=Exp[xyz];h=Sin[xyz]; gradient[f, {x,y, z}] {2x+y2+yz2, 2xy +xz2, 2xyz} jacobian[{f,g,h}, {x,y, z} ] //MatrixForm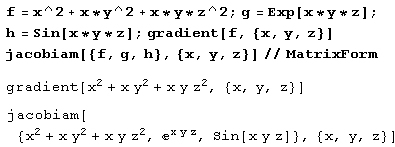
Впрочем, операции векторного анализа приходится выполнять не только в декартовой системе координат. Поэтому для выполнения этих операций имеется специальный пакет, загружаемый как обычно:
<<Calculus`VectorAnalysis`В нем предусмотрено выполнение операций в самых разнообразных системах координат – декартовой, цилиндрической, сферической, параболической, тороидальной, бисферической, сфероидальной, биполярной, параболоидной, эллиптической, эллипсоидной и т.д.
По умолчанию устанавливается декартова система координат. Вот как определить установленную систему координат и название ее переменных.
{CoordinateSystem,Coordinates[]} {Cartesian,{Xx,Yy,Zz}}Вот как вычислить градиент.
Grad[Xx+Sin[YyZz]] {1,Zz Cos[YyZz],Yy Cos[YyZz]}