Нахождение решений дифференциальных уравнений
Ниже приведен пример решения задачи Коши с помощью все той же функции:
Часто решение дифференциального уравнения имеет довольно громоздкий вид, и по нему представить поведение интегральных кривых довольно сложно. В этих случаях полезно построить график решения, т.е. вычертить интегральную кривую.
Пример 10.7. Построение графика решения дифференциального уравнения.
Решим дифференциальное уравнение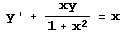 
и построим график его решения.
Сначала с помощью функции DSolve находим решение.
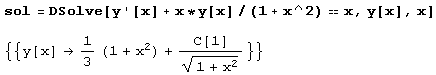
Найдя решение, можем построить его график. Для этого придется, конечно, задать значения произвольных постоянных. В данном случае это уравнение первого порядка, и потому у него только одна произвольная постоянная: с [ 1 ]. Ее значение удобнее всего задать подстановкой.
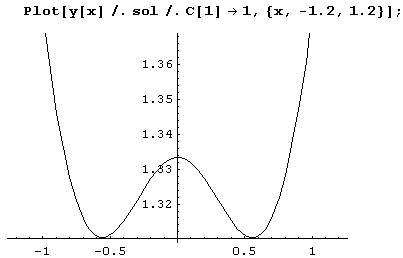
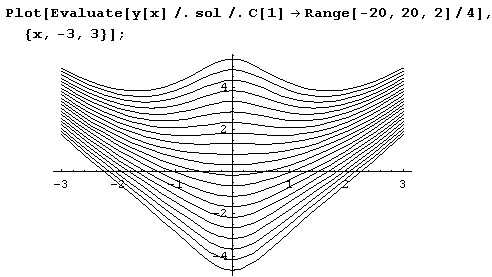
Иногда приходится строить графики решений, получающихся при различных значениях произвольных постоянных. Тогда нужно в подстановке указать список значений. Пусть, например, нужно построить графики решений для следующих значений произвольной постоянной с [ 1 ].
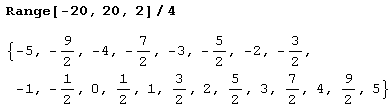
Тогда это можно сделать так.
