Интеграция Maple 7 с MATLAB
Выделение сигнала на фоне шумов
Среди небольшого числа доступных функций системы MATLAB в пакете Matlab нельзя не выделить особо функции быстрого прямого и обратного преобразований Фурье. В системе MATLAB эти функции реализуют наиболее эффективные алгоритмы быстрого преобразования Фурье (БПФ), обеспечивающие решение крупноразмерных задач (например, обработки сигналов, представленных векторами и матрицами больших размеров) в десятки раз быстрее, чем при обычных методах выполнения преобразований Фурье.
Покажем возможность применения БПФ на ставшем классическим примере – выделении спектра полезного сигнала на фоне сильных помех. Зададим некоторый двухчастотный сигнал, имеющий 1500 точек отсчета:
> num: = 1500: Time: = [seq(.03*t .t=1..num)]: data: = [seq((3.6*cos(Time[t]) + cos(6*Time[t])), t=1..num)]: plots[pointplot](zip((x,y) › [x,y],Time,data), style=line);
График сигнала представлен на рис. 15.1.
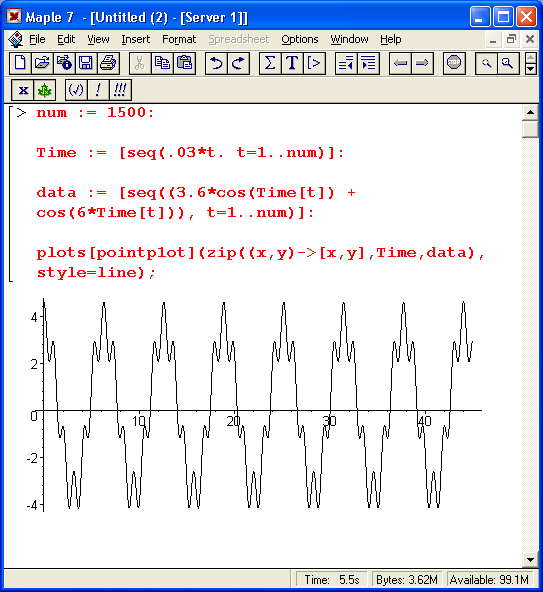
Рис. 15.1. График исходного сигнала
Теперь с помощью генератора случайных чисел наложим на этот сигнал сильный "шум" (слово "шум" взято в кавычки, поскольку речь идет 6 математическом моделировании шума, а не о реальном шуме физической природы):
> tol: = 10000: r: = rand(0..to1): noisyjlata: = [seq(r()/(tol)*data[t], t=l..num)]: plots[pointplot](zip((x,y) › [x,y],Time,noisy_data), style=line);
