Основные определения линейной алгебры
Прежде чем перейти к рассмотрению обширных возможностей пакетов Maple 7 по части решения задач линейной алгебры, рассмотрим краткие определения, относящиеся к ней.
Матрица (m х n) – прямоугольная двумерная таблица, содержащая m строк и n столбцов элементов, каждый из которых может быть представлен числом, константой, переменной, символьным или математическим выражением (расширительная трактовка матрицы).
Квадратная матрица – матрица, у которой число строк m равно числу столбцов n. Пример квадратной матрицы размера 3x3:

Сингулярная (вырожденная) матрица – квадратная матрица, у которой детерминант (определитель) равен 0. Такая матрица обычно не упрощается при символьных вычислениях. Линейные уравнения с почти сингулярными матрицами могут давать большие погрешности при решении.
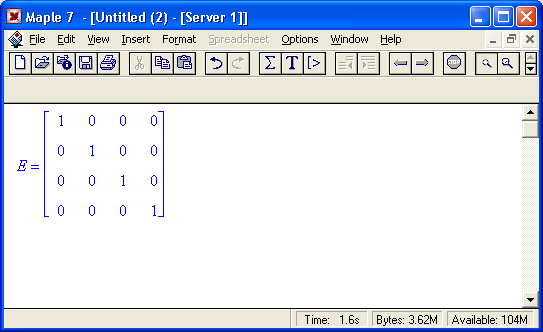
Единичная матрица – это квадратная матрица, у которой диагональные элементы равны 1, а остальные элементы равны 0. Ниже представлена единичная матрица размера 4x4:
Сингулярные значения матрицы А – квадратные корни из собственных значений матрицы АТ =А, где Ат – транспонированная матрица А (см. ее определение ниже).
Транспонированная матрица – матрица, у которой.столбцы и строки меняются. местами, то есть элементы транспонированной матрицы удовлетворяют условию AT (i,j)=A(j,i).
