Основные определения линейной алгебры
Ранг матрицы – наибольший из порядков отличных от нуля миноров квадратной матрицы.
След матрицы – сумма диагональных элементов матрицы.
Определитель матрицы – это многочлен от элементов квадратной матрицы, каждый член которого является произведением n элементов, взятых по одному из каждой строки и каждого столбца со знаком произведения, заданным четностью перестановок:
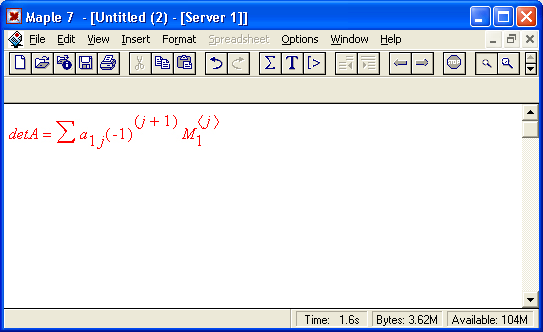
Где M1<j> – определитель матрицы порядка n -1, полученной из матрицы А вычеркиванием первой строки и j-гo столбца. В таком виде определитель (он же детерминант) легко получить в символьных вычислениях. В численных расчетах мы будем подразумевать под определителем численное значение этого многочлена.
Матрица в целой степени – квадратная матрица в степени n (n – целое неотрицательное число), определяемая следующим образом:
М° = Е, М1 = М, М2 = ММ…, Мn =Мn-1 М.
Идемпотентная матрица – матрица, отвечающая условию Р2 = Р.
Симметрическая матрица – матрица, отвечающая условию Ат = А.
Кососимметрическая матрица – матрица, отвечающая условию Ат = -A.
Ортогональная матрица – матрица, отвечающая условию Ат =А-1.
Нуль-матрица – матрица, все элементы которой равны 0.
Блок-матрица – матрица, составленная из меньших по размеру матриц, также можно представить как матрицу, каждый элемент которой – матрица. Частным случаем является блок-диагональная матрица – блок-матрица, элементы-матрицы которой вне диагонали – нуль-матрицы.
Комплексно-сопряженная матрица – матрица А, полученная из исходной матрицы А заменой ее элементов на комплексно-сопряженные.
Эрмитова матрица – матрица А, удовлетворяющая условию А = А.
Собственный вектор квадратной матрицы А – любой вектор х е V", х* О, удовлетворяющий уравнению Ах = gx, где g – некоторое число, называемое собственным значением матрицы А.
Характеристический многочлен матрицы – определитель разности этой матрицы и единичной матрицы, умноженный на переменную многочлена, – |А -gE|.
Собственные значения матрицы – корни ее характеристического многочлена.
Норма – обобщенное понятие абсолютной (величины числа. Норма трехмерного вектора ||х|| – его длина.
Норма матрицы – значение sup(||Ax||/||x||).
Матричная форма записи системы линейных уравнений – выражение АХ = В, где А – матрица коэффициентов системы, X – вектор неизвестных и В – вектор свободных членов.
Один из способов решения такой системы очевиден – X = А-1 В, где А-1 – обратная матрица.