Пакет для работы с полиномами PolynomialTools
Обзор возможностей пакета PolynomialTools
Пакет для работы с полиномами PolynomialTools предназначен для выполнения ряда специальных операций с полиномами или создания полиномов с заданными свойствами. Этот пакет имеет небольшое число функций:
> with(PolynomialTools): [IsSelfReciprocal, MinimalPolynomial, PDEToPolynomial, PolynomialToPDE, Shorten, Shorter, Sort, Split, Splits, Translate]
В пакет входят функции расщепления, сортировки и преобразования полиномов (в том числе в дифференциальные уравнения и наоборот) и др.
Функции для работы с полиномами
Рассмотрим несколько функций пакета PolynomialTools общего характера. Примеры применения этой функции представлены ниже:
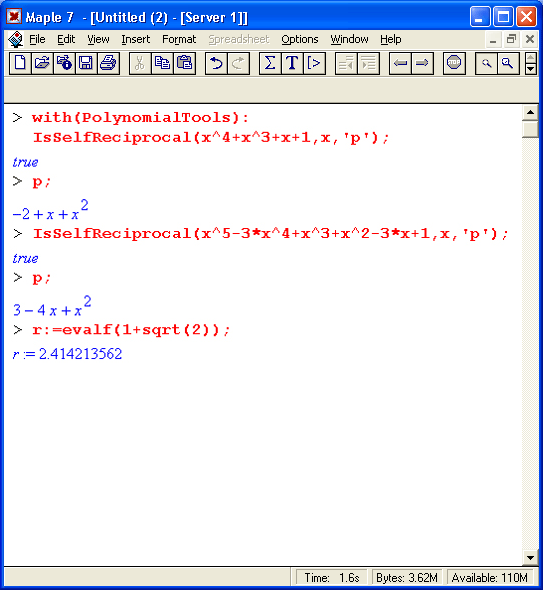
Примечание
Функция IsSelfReciprocat(a, х, 'р') проверяет полином а(х) на условие coeff(a,x,k) =coeff(a,x,d-k) для всех k = 0..d, где d = degree(a; х) – порядок полинома. Если это условие выполняется, то возвращается логическое значение true, иначе – false. Если порядок d четный и если задан третий аргумент р, то р будет представлять полином Р порядка d/2, такой, что x^(1/2)*P(x+1/x) = а. При нечетном d полином а будет взаимообратным, что подразумевает деление на х+1. В этом случае, если р указано, результат вычисляется в форме а/(х+1).
