Пакет ортогональных многочленов orthopoly
Ортогональные многочлены (полиномы) находят самое широкое применение в различных математических расчетах. В частности, они широко используются в алгоритмах интерполяции, экстраполяции и аппроксимации различных функциональных зависимостей. В пакете orthopoly задано в функции:
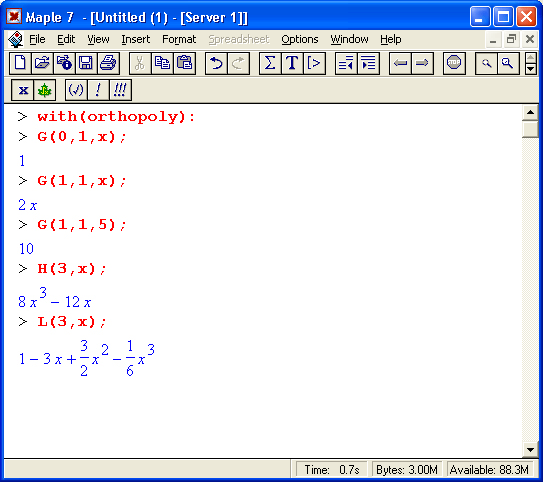
> with(orthopoly); [G,H,L,P,T,U]
Однобуквенные имена этих функций отождествляются с первой буквой в наименовании ортогональных полиномов. Вопреки принятым в Maple 7 правилам, большие буквы в названиях этих полиномов не указывают на инертность данных функций – все они являются немедленно вычисляемыми. В данном разделе функции этого пакета будут полностью описаны.
Отметим определения указанных функций:
- G(n,a,x) – полином Гегенбауэра (из семейства ультрасферических полиномов);
- Н(n,х) – полином Эрмита;
- L(n,x) – полином Лагерра;
- L(n,а,х) – обобщенный полином Лагерра;
- Р(n,х) – полином Лежандра;
- P(n,a,b,x) – полином Якоби;
- Т(n,х) – обобщенный полином Чебышева первого рода;
- U(n,x) – обобщенный полином Чебышева второго рода.
Свойства ортогональных многочленов хорошо известны. Все они характеризуются целочисленным порядком n, аргументом х и иногда дополнительными параметрами а и b. Существуют простые рекуррентные формулы, позволяющие найти полином n-го порядка по значению полинома (n -1)-го порядка. Эти формулы и используются для вычисления полиномов высшего порядка.
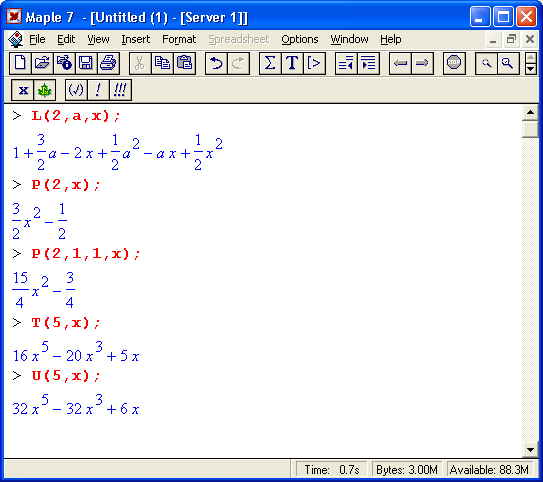
Ниже представлены примеры вычисления ортогональных полиномов: