Пакет ортогональных многочленов orthopoly
Наконец, на рис. 14.3 даны графики ортогональных многочленов Чебышева Т(n, х) и U(n, х).
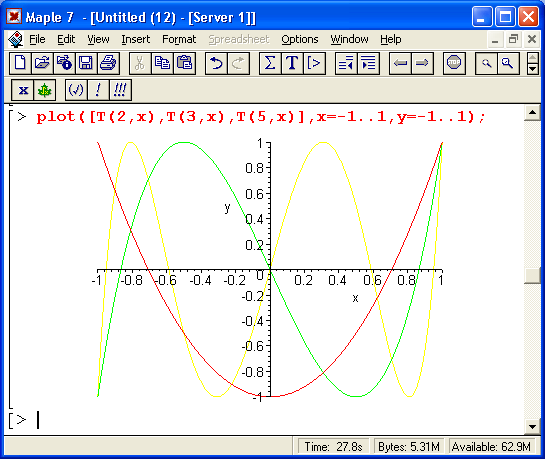
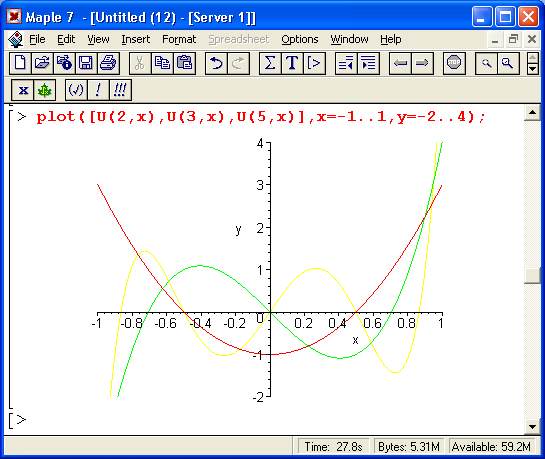
Рис. 14.3. Графики ортогональных многочленов Чебышева
Приведенные графики дают начальное представление о поведении ортогональных многочленов.
К примеру, многочлены Чебышева имеют минимальное отклонение от оси абсцисс в заданном интервале изменениях. Это их свойство объясняет полезное применение таких многочленов при решении задач аппроксимации функций. Можно порекомендовать читателю по их образу и подобию построить графики ортогональных многочленов при других значениях параметра и и диапазонах изменения аргумента х.
В отличие от ряда элементарных функций ортогональные многочлены определены только для действительного аргументах. При комплексном аргументе просто повторяется исходное выражение с многочленом:
> evalf(U(2.2+3*I))): Р(2.2 + 3I) > evalf(sqrt(2+3*I))); 1.674149228+.8959774761I
Ортогональные многочлены неопределены также и для дробного показателя n. Впрочем, надо отметить, что такие многочлены на практике используются крайне редко.
