Коэффициенты уверенности и условные вероятности
Предположим, что вероятности имеют следующие значения:
P(d1) = 0.8,
P(d2) = 0.2,
P(d1|e) = 0.9,
P(d2| e) = 0.8.
Тогда повышение доверия к d1 будет равно (0.9-0.8) / 0.2 = 0.5, а повышение доверия к: d2 -(0.8-0.2) / 0.8 = 0.75.
Отсюда следует, что CF(d1| e) < CF(d2, е), несмотря на то, что и P(d1 | e) > P(d2| е).
Адаме назвал это явление "нежелательным свойством" коэффициентов доверия. Избежать такой ситуации можно, если все априорные вероятности будут равны. Несложно показать, что эффект в приведенном выше примере явился следствием того, что признак е больше свидетельствовал в пользу гипотезы d2, чем в пользу d1, именно из-за более высокой априорной вероятности последней. Однако приравнивание априорных вероятностей явно не согласуется со стилем мышления тех, кто ставит диагноз, поскольку существует достаточно большое отличие в частоте сочетаний разных болезней с одинаковыми симптомами, следовательно, эксперты будут присваивать им совершенно разные значения субъективных вероятностей.
Последовательное применение правил в системе MYCIN также связано с существованием определенных теоретических проблем. Используемая при этом функция комбинирования основана на предположении, что если признак е влияет на некоторую промежуточную гипотезу h с вероятностью P(h | е), а гипотеза h входит в окончательный диагноз d с вероятностью P(d | h), то:
P(d|e) = P(d|h)P(h|e).
Таким образом, создается впечатление, что транзитивное отношение в последовательности правил вывода суждений справедливо на первом шаге, но не справедливо в общем случае. Для того чтобы существовала связь между правилами, популяции, связанные с этими категориями, должны быть вложены примерно так, как на рис. 9.1.
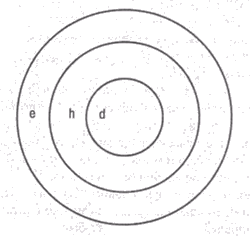
Рис. 9.1. Популяции, позволяющие использовать P(d | е; = P(d| h)P(h| z)
Адаме пришел к выводу, что успех практического применения системы MYCIN и других подобных систем объясняется тем, что в них используются довольно короткие последовательности комбинирования правил, а рассматриваемые гипотезы довольно просты.
Другое критическое замечание относительно MYCIN было высказано Горвицем и Гекерманом и касается использования коэффициентов уверенности в качестве меры изменения доверия, в то время как в действительности они устанавливаются экспертами в качестве степени абсолютного доверия [Horvitz and Heckerman, 1986]. Связывая коэффициенты доверия с правилами, эксперт отвечает на вопрос: "Насколько вы уверены в правдоподобности того или иного заключения?" При применении в MYCIN функций комбинирования дополнительных признаков эти коэффициенты становятся мерой обновления степени доверия, что приводит к несовместимости этих значений с теоремой Байеса.
