Иллюстрированный самоучитель по введению в экспертные системы

Методика Перла

Но, хотя Перл использует формализм Байеса, частичное свидетельство в пользу какой-либо гипотезы не может быть истолковано и как частичная поддержка отрицания этой гипотезы. Свидетельство в пользу подмножества гипотез S не может быть истолковано как свидетельство в пользу дополнения к этому подмножеству 5^е.

Распределение свидетельств в пользу подмножества между отдельными гипотезами восстанавливает точечное распределение вероятностей на пространстве гипотез, но это происходит за счет точности оценок для отдельных гипотез. Перл утверждает, что нет необходимости распределять общий показатель, взятый для всего подмножества S, на его элементы до тех пор, пока не будут получены дополнительные свидетельства (или все возможные). Нормализацию также можно отложить до тех пор, пока полученные свидетельства не подтолкнут систему к выделению определенных гипотез (возможно, разных). Например, если получены свидетельства Е₁,…, Е_n соответственно в пользу гипотез S₁,…, S_n, то веса будут комбинироваться мультипликативно:

W_i(E₁,…,E_n)=W_1,i,W_2,i… W_n,i, где W_k,i =л_Sk если hi 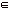S_k, иначе 1.

Перл предложил также и альтернативный механизм обновления, который позволяет обойтись без нормализации и включает распространение пересмотра параметров гипотез как вверх, так и вниз по иерархической структуре с помощью передачи сообщений. С точки зрения практической реализации этот механизм кажется более привлекательным, чем правило Демпстера. Перл утверждает, что метод распространения, основанный на передаче сообщений, достаточно прозрачен, поскольку пути влияния имеют семантическое обоснование. Отказ от глобальной нормализации позволяет лучше понять результаты на промежуточных этапах распространения. Остается только один числовой параметр – отношение вероятностей, – смысл которого достаточно понятен.

Байесовские сети

В работе [Pearl, 1988] описан формализм, которому автор присвоил название Байесовские сети. Этот механизм можно рассматривать как обобщение описанных в данном разделе иерархических сетей доверия. В Байесовской сети дуги между узлами также представляют причинные зависимости, но допускается ситуация, когда некоторые узлы имеют множество родителей, причем структура сети может содержать петли. Обновление оценок доверия выполняется с помощью передачи сообщений, как и в случае строгой иерархической организации, хотя действие этого механизма очевидно только для полидеревьев, т.е. сетей, в которых между любыми двумя узлами существует единственный путь.

Представляет интерес сравнение формализма Перла и теории Демпстера-Шефера.

• В системе Перла нужно присваивать априорные оценки доверия отдельным событиям, а в теории Демпстера-Шефера оценка распространяется на всю область анализа.
• В системе Перла определение функции ВЕL(h₁) через P(h₁) и BEL'(h₁) через P(h, | E) позволяет более корректно обосновать эти функции на основе выводов теории вероятностей, чего нельзя сказать о правилах комбинирования Демпстера, с чем согласился и Шефер в работе [Shafer, 1976].
• Йен [Yen, 1986] обратил внимание на то, что в формализме Перла теряется понятие доверительного интервала, внутри которого могут изменяться вероятностные оценки. Доверительные интервалы очень удобно использовать в экспертных системах, поскольку они позволяют судить о "качестве" гипотез, возможности их совершенствования и ассоциированной степени неопределенности.

В своей книге [Pearl, 1988] Перл совершенно справедливо отмечает, что теория Демпстера-Шефера основана на неполной вероятностной модели, а потому может дать только частичные ответы. Вместо того чтобы непосредственно оценить, насколько близка гипотеза к тому, чтобы ее можно было считать истинной, эта теория говорит, как сильно полученное свидетельство должно продвинуть нас к убеждению, что данная гипотеза истинна. В этом отношении теория Демпстера-Шефера значительно больше напоминает объективистские методы проверки значимости с использованием доверительных интервалов, чем субъективистские методы на основе Байесовского подхода [Neapolitan, 1990].

Но, несмотря на отмеченные различия, в обоих подходах есть много общего, почему мы и рассматриваем их совместно в рамках одной главы. Ассоциирование свидетельств с подмножествами гипотез в рамках метода Перла не противоречит отображению одного множества на другое в теории Демпстера-Шефера. Оба варианта можно рассматривать как использование метафоры "массового распределения" в том смысле, что основное внимание уделяется распределению полученных свидетельств в контексте структурированного пространства альтернатив, причем оба метода позволяют вычислять значения функции доверия на основе простых вероятностных оценок.