Иллюстрированный самоучитель по введению в экспертные системы

Рекомендуемая литература. Упражнения.

В своей книге [Pearl, 1988] Перл уделяет основное внимание методам, основанным на Байесовском подходе, демонстрируя их возможности на множестве примеров, взятых из различных областей искусственного интеллекта. Эту книгу можно рекомендовать в качестве отправной точки для детального изучения проблемы обработки неопределенности в задачах искусственного интеллекта, поскольку изложенный в ней материал является самодостаточным. Структура книги позволяет читателям с разным уровнем подготовки выбирать нужный для себя материал. Более поздняя работа [Pearl, 1997] содержит описание последних исследований в этой области, включая и теорию сетей доверия. Среди других книг на эту тему я бы выделил [Jensen, 1996] и [Shafer and Pearl, 1990].

Упражнения

Упражнение 1
На рис. 21.1 приведена схема простого пространства гипотез для задачи поиска неисправности в автомобиле. Корневой узел, неисправность автомобиля, представляет множество неисправностей {неисправность системы подачи топлива, неисправность электрооборудования}. Узел неисправность системы подачи топлива представляет множество {неисправность карбюратора, неисправность бензопровода}, а узел неисправность электрооборудования – множество {неисправность аккумуляторной батареи, неисправность распределителя}. Таким образом, узел неисправность автомобиля можно рассматривать как представляющий всю область анализа.

Э = {неисправность системы подачи топлива, неисправность электрооборудования, неисправность карбюратора, неисправность бензопровода}.

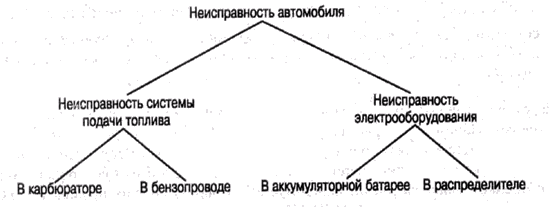
Рис. 21.1. Пространство гипотез о неисправностях в автомобиле

I) Предположим, что степень подтверждения диагноза неисправность карбюратора имеющимися свидетельствами оценивается значением 0.8. Вычислите т(неисправность бензопровода), т(неисправность электрооборудования) и m(0).

II) Предположим, что степень опровержения диагноза неисправность системы подачи топлива имеющимися свидетельствами оценивается значением 0.6. Вычислите т{неисправность электрооборудования).

Ill) Предположим, что степень подтверждения диагноза неисправность карбюратора имеющимися свидетельствами оценивается значением 0.2, а диагноза неисправность бензопровода – значением 0.5. Вычислите т(неисправность системы подачи топлива).

Упражнение 2
Используя пространство гипотез, представленное на рис. 21.1, предположим, что степень подтверждения диагноза неисправность системы подачи топлива имеющимися свидетельствами оценивается значением 0.3, а диагноза неисправность аккумуляторной батареи – значением 0.6. Вычислите значения т для всех узлов графа, используя правило Демпстера.

Упражнение 3
Пусть на пространстве гипотез, представленном на рис. 21.1, априорные вероятности отдельных гипотез равны:

Р(неисправность карбюратора) = 0.4;

Р(неисправность бензопровода) = 0.1;

Р(неисправность аккумуляторной батарей) = 0.3.

Предположим, что имеется свидетельство е, такое, что:

Р(е| неисправность карбюратора) = 0.3;

Р(е| – неисправность карбюратора) = 0.5;

Р(е| неисправность бензопровода) = 0.2;

Р(е| – (Неисправность бензопровода) = 0.4;

Р(е| неисправность аккумуляторной батареи) = 0.6;

Р(е| – (Неисправность аккумуляторной батареи) – 0.3;

Р(е| неисправность распределителя) = 0.7;

Р(е| – (неисправность распределителя) = 0.1.

Вычислите новые значения оценок доверия к каждой из гипотез, используя метод Перла.