Иллюстрированный самоучитель по введению в экспертные системы

Методика Перла

Альтернативой теории Демпстера-Шефера является методика Перла [Pearl, 1986], в которой свидетельства учитываются на основе Байесовского подхода к группированию и распространению влияния свидетельств на достоверность гипотез. Как и в методике, предложенной Гордоном (Gordon) и Шортлиффом (Shortliffe), предполагается, что в пространстве гипотез выделено некоторое подмножество гипотез, представляющих интерес в определенном семантическом контексте, причем это подмножество имеет иерархическую структуру.

Предполагается также, что еще до получения свидетельств с каждой отдельной гипотезой связано определенное значение степени доверия к ее правдоподобности. Перл не уточняет, каким именно способом формируются эти исходные значения, но скорее всего это должен сделать эксперт в предметной области при формулировке гипотез.

От эксперта также требуется выделить множество гипотез S, на которые непосредственно распространяется определенное множество свидетельств Е. Если свидетельства из Е непосредственно влияют на гипотезы из S, то должен существовать какой-то причинный механизм, связывающий каждый член множества S со свидетельствами, причем он является уникальным для каждого из них. Однако сами по себе свидетельства в множестве Е не несут никакой информации, которая позволила бы нам отдать предпочтение одному из членов S перед другими.

Это отображение множеств друг на друга позволяет ввести понятие условной независимости между свидетельствами и отдельными гипотезами h_i:

Р(Е | S, h_i) = Р(Е | S, h₁), для всех h_i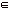 S.

С помощью отношения вероятностей можно количественно оценить степень, с которой свидетельства подтверждают или опровергают множество гипотез S:лS=[P(E|S)] / [P(E|-S)].

Влияние свидетельств Е на множество S вычисляется следующим образом. Каждая отдельная гипотеза h_i, принадлежащая множеству S, получает вес W_i = л_S , в то время как каждая гипотеза из дополняющего множества S^C получает вес W_i = 1. Все это выполняется на фазе распределения весов.

Затем, когда наступает фаза обновления, вычисляется новое значение функции доверия ВЕL'(h_i) по ее прежнему значению ВЕL(h_i):

BEL'(h_i) = P(h_i | Е) = a _s W_iВЕL(h_i), где a _s – коэффициент нормализации, заданный соотношением a _s =(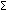 _i[W_iBEL'(h_i))^-1. ].

Таким образом, степень доверия, назначенная множеству гипотез, распределяется между членами этого множества как функция их априорных вероятностей. В то же время степень доверия, назначенная группе гипотез, является суммой соответствующих показателей элементов этой группы. Обновление значений показателей доверия может выполняться рекурсивно, т.е. апостериорные оценки, полученные на основании одних свидетельств, могут использоваться в качестве априорных оценок для следующего цикла обновления при получении новых свидетельств.

Вся схема вычислений основана на предположении об условной независимости и соблюдении симметричности множеством S^C, дополняющим S. Из соотношения:

Р(Е | S^C, h_i) = Р(Е | S^C, h_i) для всех h_i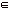 S^C следует, что Р(Е | h_i) = Р(Е | S), если h_i, h_i 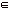S, иначе Р(Е | S^C).

Из этого соотношения и правила Байеса следует, что P(h,| Е) = a_sX_sP(h,), если Л, е S, иначе a_sP(h,).