Иллюстрированный самоучитель по введению в экспертные системы

Функции доверия

В теории Демпстера-Шефера т – это функция присвоения базовых вероятностей (bра – basic probability assignment), которая определена на множестве 2^O значений из интервала [0.1], такая,
что: m(пустое множество) = 0 и 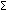[(т(Аi) -1]; суммирование выполняется по всем A_i 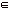2^O.

Суммарное доверие Bel для любого фокального элемента А может быть найдено суммированием значений т по всем подмножествам в А. Таким образом, Bel является функцией, определенной на множестве 2^е значений из интервала [0.1], такой, что: Bel(A) = 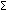_{B 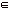A}m(B).

Веl(0) всегда равно 1, независимо от значения т(O). Это следует из определения функции присвоения базовых вероятностей. Соотношение Веl(O) = 1 означает следующее: можно с полной уверенностью утверждать, что в пространстве 0 обязательно имеется корректная гипотеза, поскольку по определению набор гипотез является исчерпывающим. Значение m(O) отображает вес свидетельства, еще не учтенного в подмножествах, входящих в пространство 0. Значения Bel и т будут равны для множеств, состоящих из единственного элемента.

Оценка вероятности фокального элемента А будет ограничена снизу оценкой доверия к А, а сверху – оценкой привлекательности А, которая равна 1 -Веl(A^с) >, где A^с – дополнение к A.

Оценка привлекательности A, Рls(A), представляет степень совместимости свидетельства с гипотезами в А и может быть вычислена по формуле:

Рls(A)= 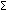_{A^B не равно пустому множеству} m(B).

Поскольку определенная таким образом оценка привлекательности А есть не что иное, как мера нашего недоверия к -A, то можно записать:

Рls (A) = 1 -Вel (-A).

Значение оценки привлекательности А можно рассматривать как предел, до которого можно улучшить гипотезы из А при наличии свидетельств в пользу гипотез-конкурентов. Удобно рассматривать информацию, содержащуюся в оценке Bel для данного подмножества, в виде доверительного интервала в форме [Вel(A), Pls(A)]. Ширина интервала может служить оценкой неуверенности в справедливости гипотез из А при имеющемся наборе свидетельств.

Правила Демпстера позволяют вычислить новое значение функции доверия по двум ее значениям, базирующимся на разных наблюдениях. Обозначим Bel₁ и Веl₂ два значения функции доверия, которым соответствуют два значения функции присвоения базовых вероятностей т₁ и т_г. Правило позволяет вычислить новое значение т₁+т₂, а затем и новое значение функции доверия Веl₁+ Веl₂, основываясь на определениях, приведенных выше.

Для гипотезы А значение т₁+т₂(А) есть сумма всех произведений в форме т₁(Х) m₂(Y), где X и Y распространяются на все подмножества в в, пересечением которых является А. Если в таблице пересечений будет обнаружен пустой элемент, выполняется нормализация. В процедуре нормализации значение k определяется как сумма всех ненулевых значений, присвоенных в множестве 0, затем т₁+т₂(0) присваивается значение нуль, а значения m₁+m₂ для всех других множеств гипотез делится на (1 -k).

Таким образом, m₁+m₂= 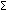_X^Y=A[m₁(X)m₂(Y)]/[1 - 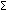X^Y=пустое множество { m₁(X)m₂(Y) }].

Следует учитывать, что значения т₁ и m₂ сформированы по независимым источникам свидетельств в пределах того же пространства гипотез. Обратите внимание и на тот факт, что вследствие коммутативности операции умножения правило Демпстера дает один и тот же результат при любом порядке объединения свидетельств.