Повороты и параллельные сдвиги
Предположим, что в оригинале присутствует какая-либо четкая вертикальная линия, которая может являться штрихом символа или каким-то элементом изображения (вертикалью угла стены или колонны). Если такое изображение повернуть не на 90 градусов (или углы, кратные 90 градусам), то, естественно, что этот четкий и ясный элемент, попадающий в сетку дискретизации, приобретет совсем иной вид (рис. 11.19).


Рис. 11.19. Поворот вертикальной и горизонтальной границы на угол в 30 градусов (увеличено)
Такой вид связан с тем, что сетка дискретизации никогда не изменяет своей ортогональности. Поэтому повороты пиксельного изображения на произвольные углы всегда происходят с погрешностями. Другое дело, что в некоторых случаях зритель может их просто не заметить.
Замечание
Стоит обратить внимание на то, что эти погрешности касаются не только повернутого изображения, они характерны также для наклонных или округлых элементов. Причина у них одна – несовпадение сетки дискретизации со структурой элементов изображения.
Параллельные сдвиги
Параллельные сдвиги, превращающие прямоугольник в параллелограмм или в ромб, являются вариантами поворотов и имеют абсолютно идентичные погрешности (рис. 11.20).
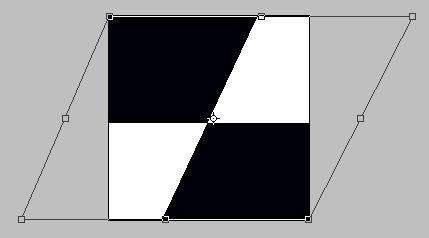
Рис. 11.20. Пример параллельного сдвига по горизонтали
