XY-график вектора и ранжированной переменной. XY-график функции. Полярный график.
В качестве переменных, откладываемых по любой из осей, можно использовать саму ранжированную переменную (рис. 16.5). При этом по другой оси должно быть отложено либо выражение, явно содержащее саму ранжированную переменную, либо элемент вектора с индексом по этой ранжированной переменной, но никак не сам вектор.
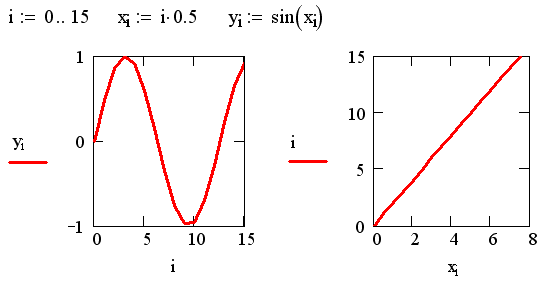
Рис. 16.5. Графики вектора и ранжированной переменной
XY-график функции
Нарисовать график любой скалярной функции f (х) можно двумя способами. Первый заключается в дискретизации значений функции, присвоении этих значений вектору и прорисовке графика вектора. Собственно, так и были получены графики синуса на рис. 16.3-16.5. Второй, более простой способ, называемый быстрым построением графика, заключается во введении функции в один из местозаполнителей (например у оси Y), а имени аргумента – в местозаполнитель у другой оси (рис. 16.6). В результате Mathcad сам создает график функции в пределах значении аргумента, по умолчанию принятых равными от -10 до 10. Разумеется, впоследствии можно поменять диапазон значений аргумента, и график автоматически подстроится под него.
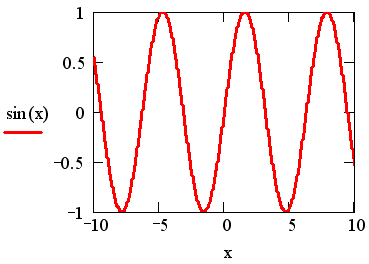
Рис. 16.6. Быстрое построение графика функции
Необходимо заметить, что если переменной аргумента функции было присвоено некоторое значение до построения в документе графика, то вместо быстрого построения графика будет нарисована зависимость функции с учетом этого значения. Примеры двух таких графиков приведены на рис. 16.7.
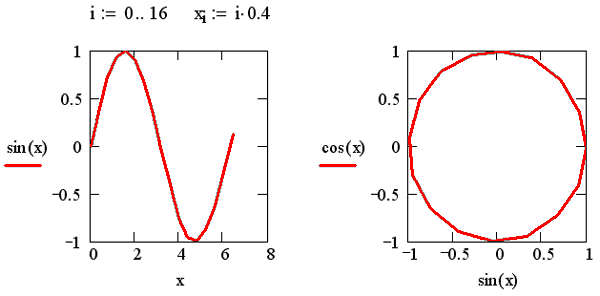
Рис. 16.7. Графики функций от векторного аргумента
Полярный график
Для создания полярного графика необходимо нажать кнопку Polar Plot на панели Graph (График) (рис. 16.8) и вставить в местозаполнители имена переменных и функций, которые будут нарисованы в полярной системе координат угол (нижний местозаполнитель) и радиус-вектор (левый местозаполнитель).
Точно так же, как при создании Декартова графика (см. разд. 163.1-16.3.3), по осям могут быть отложены два вектора (рис. 16.8, слева), элементы векторов и ранжированные переменные в различных сочетаниях, а также может быть осуществлено быстрое построение графика функции (рис. 16.8, справа).
Форматирование полярных графиков практически идентично форматированию Декартовых, поэтому все, сказанное ниже об оформлении двумерных графиков на примере XY-графиков, в полной мере относится и к полярным.
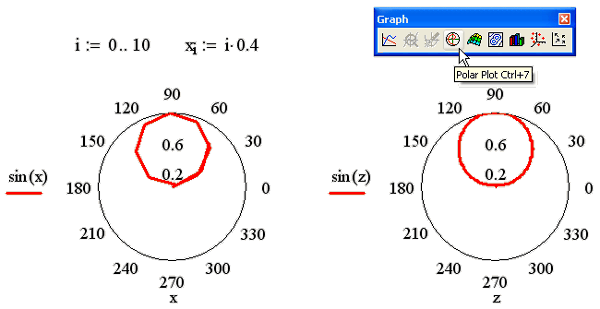
Рис. 16.8. Полярные графики
