Функции Бесселя
Естественно, что возможно построение графиков специальных функций.
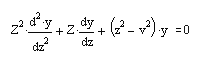
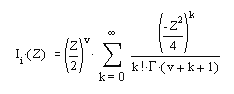
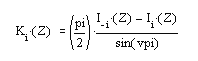
В качестве примера рассмотрим m-файл-сценарий, приведенный ниже:
x=0:0.1:10; y0=besselj(0.x); y1=besselj(1.x): y2=besselj(2.x); y3=besselj(3.x); plot(x,y0,.'-m',x,y1,'-r',x,y2,'-.k',x,y3,'-b') legend('besselj(0.x)'. 'besselj(l.x)','besse1j(2,x)'. (besselj(3,x)');Рисунок 9.1 иллюстрирует построение четырех функций Бесселя bessel j(n,x) для n – 0, 1, 2 и 3 с легендой, облегчающей идентификацию каждой кривой рисунка.
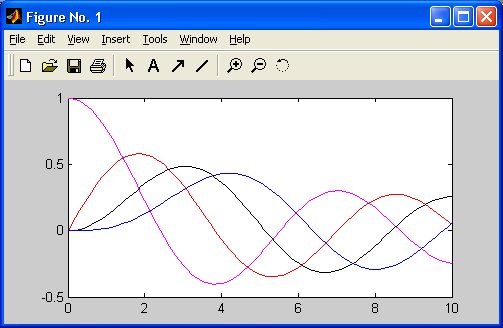
Рис. 9.1. Графики четырех функций Бесселя besselj(n,x)
Эти графики дают наглядное представление о поведении функций Бесселя, широко используемых при анализе поведения систем, описываемых линейными дифференциальными уравнениями второго порядка.
