Гамма-функция и ее варианты
Гамма-функция определяется выражением:
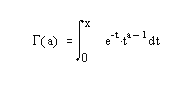
Неполная гамма-функция определяется как:
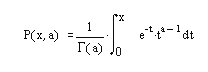
- gamma (А) – возвращает гамма-функцию элементов А. Аргумент А должен быть вещественным.
- gamma inc(X,А) – возвращает неполную гамма-функцию соответствующих элементов X и А. Аргументы X и А должны быть вещественными и иметь одинаковый размер (или любой из них может быть скалярным).
- gammaln(A) – возвращает логарифмическую гамма-функцию, gammaln(A) = log(gamma(A)). Команда gammaln позволяет избежать переполнения, которое может происходить, если вычислять логарифмическую гамма-функцию непосредственно, используя log(gamma(A)).
Примеры:
>> f=[5.3];d=gamma(f) d =24 2>> h=gammaln(f) h =3.1781 0.6931Гамма-функция имеет довольно "сложный", график, заслуживающий построения (рис. 9.2).
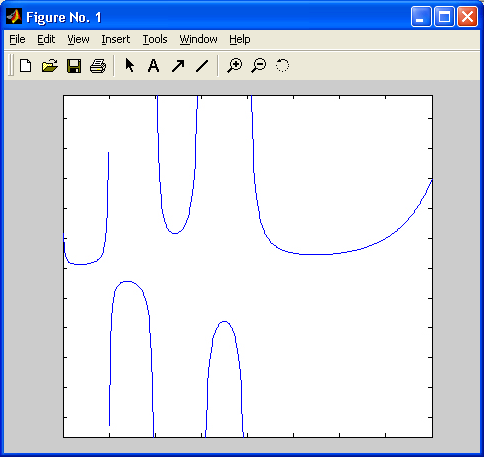
Рис. 9.2. График гамма-функции
Это можно осуществить с помощью следующего файла-сценария:
%Gamma function graphicclear syms x ezplot(gamma(x).[-4 4]) grid onГамма-функция вычисляется по известному алгоритму W. J. Kody (1989 г.). Для вычисления неполной гамма-функции используются рекуррентные формулы.
