Функции ошибки. Интегральная показательная функция.
Функция ошибки определяется следующим образом:
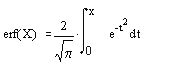
- erf(X) – возвращает значение функции ошибки для каждого элемента вещественного массива X. Дополнительная (остаточная) функция ошибки задается соотношением:
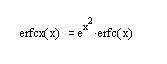
- erfc(X) – возвращает значение остаточной функции ошибки.
- erfcx(X) – возвращает значение масштабированной остаточной функции ошибки. Эта функция определяется так:
егfсх(х) = ех erfc(x).
- erfinv(Y) – возвращает значение обратной функции ошибки для каждого элемента массива Y. Элементы массива Y должны лежать в области – 1<Y<1. Примеры:
>> Y=[0.2,-0.3];a=erf(Y) a =0.2227-0.3286>> b=erfc(Y) b =0.7773 1.3286>> c=erfcx(Y) c =0.8090 1.4537>> d=erfinv(Y) d =0.1791-0.2725При вычислении данных функций используется аппроксимация по Чебышеву (см. детали алгоритма в Reference Book по MATLAB).
Интегральная показательная функция
Интегральная показательная функция определяется следующим образом:
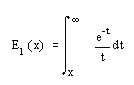
- expint(X) – возвращает интегральную показательную функцию для каждого элемента X. Пример:
>> d=expint([2.3+7i]) d =0.0489-0.0013-0.00601Для вычисления этой функции используется ее разложение в ряд.
