Иллюстрированный самоучитель по MatLab

Эллиптические функции и интегралы

Эллиптические функции Якоби определяются интегралом и соотношениями:

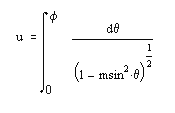
• сn(u) = cos ф,
• cn(u)=cosф,
• dn(u) = (1-sin² ф)^1/2,
• аm(u) = ф.

В некоторых случаях при определении эллиптических функций используются модули k вместо параметра гл. Они связаны выражением k = т = sin a.

• [SN.CN.DN] = ellipj(U.M) – возвращает эллиптические функции Якоби SN, CN и. DN, вычисленные для соответствующих элементов – аргумента U и параметра М. Входные величины U и М должны иметь один и тот же размер (или любая из них может быть скаляром).
• [SN.CN.DN] = ellipj(U,M,to1) – возвращает эллиптическую функцию Якоби, вычисленную с точностью tol. Значение tol по умолчанию – eps; его можно увеличить, тогда результат будет вычислен быстрее, но с меньшей точностью. Пример:

Полные эллиптические интегралы первого и второго рода определяются следующим образом:

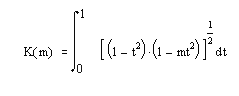
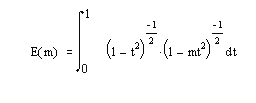
• ellipke(M) – возвращает полный эллиптический интеграл первого рода для элементов М.
• [К.Е] = ellipke(M) – возвращает полные эллиптические интегралы первого и второго рода.
• [К.Е] = ellipke(M.tol) – возвращает эллиптические функции Якоби, вычисленные с точностью tol. Значение по умолчанию – eps; его можно увеличить, тогда результат будет вычислен быстрее, но с меньшей точностью. Пример:

Для вычисления этих функций используется итерационный метод арифметико-геометрического среднего (см. детали в Reference Book по системе MATLAB).