Иллюстрированный самоучитель по MatLab

Ортогональные полиномы Лежандра

Функция Лежандра определяется следующим образом:

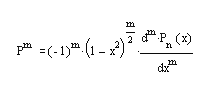
Где Рn(*) – полином Лежандра степени n, рассчитываемый как:

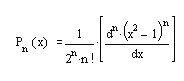
• legendre(n.X) – возвращает функции Лежандра степени п и порядков m = 0.1…. .n, вычисленные для элементов X. Аргумент п должен быть скалярным целым числом, не превосходящим 256, а X должен содержать действительные значения в области – UxJl. Возвращаемый массив Р имеет большую размерность, чем X, и каждый элемент P(m+1,d1,d2…) содержит связанную функцию Лежандра степени п и порядка т, вычисленную в точках X(d1,d2…).
• legendre(n,X, 'sch') – возвращает квазинормализованные по Шмидту функции Лежандра.

Пример:

Что нового мы узнали?

В этом уроке мы научились:

• Вычислять функции Эйри.
• Вычислять функции Бесселя разного рода.
• Вычислять бета-функцию и ее варианты.
• Использовать эллиптические функции и интегралы.
• Вычислять функции ошибки.
• Вычислять интегральные показательные функции.
• Вычислять гамма-функцию и ее варианты.
• Использовать ортогональные полиномы Лежандра.