Иллюстрированный самоучитель по MatLab

Функции Эйри

Специальные математические функции являются решениями дифференциальных уравнений специального вида или обозначениями некоторых видов интегралов. Довольно полный обзор специальных функций дается в книгах, так что ниже мы ограничимся только указанием функций системы MATLAB, реализующих их вычисление. Набор специальных математических функций в системе MATLAB настолько представителен, что позволяет решать практически все задачи, связанные с применением таких функций. Если и обнаруживаются недостающие специальные функции, то пользователь может сам задать их вычисления. Специфика специальных функций в MATLAB та же, что и элементарных, – их аргументами могут быть как одиночные численные значения, так и массивы чисел. В последнем случае функции возвращают массив тех же размерности и размера с преобразованием каждого элемента в соответствии с действием функции. В версии MATLAB 6 вы теперь можете получить справку с записью формул в стандартной математической форме, набрав в командной строке doc function, где function – имя специальной функции.

Функция Эйри формирует пару линейно независимых решений линейного дифференциального уравнения вида:

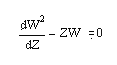
Связь между функцией Эйри и модифицированной функцией Бесселя выражается следующей формулой:

Где:

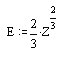
• airy(Z) – возвращает функцию Эйри, AKZ), для каждого элемента комплексного массива Z;
• airy(k.Z) – возвращает различные варианты результата в зависимости от значения k:
  • k=0 – тот же результат, что и airy(Z);
  • k=1 – производную от А1 (Z);
  • k=2 – функцию Эйри второго рода, 61 (Z):
  • k=3 – производную от B1(Z). Пример: