Иллюстрированный самоучитель по MatLab

Функции Бесселя

Линейное дифференциальное уравнение второго порядка вида:

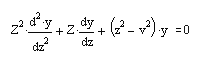
Где v – неотрицательная константа, называется уравнением Бесселя, а его решения известны как функции Бесселя. Функции J _v (z) и J_ _v (z) формируют фундаментальное множество решений уравнения Бесселя для неотрицательных значений п (это так называемые функции Бесселя первого рода): где для гамма-функции используется следующее представление:

Второе решение уравнения Бесселя, линейно независимое от J _v (z), определяется как и задает функции Бесселя второго рода Y_v(z).

Функции Бесселя третьего рода (функции Ханкеля) и функция Бесселя первого и второго рода связаны следующим выражением:

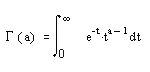
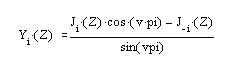
• besselj(nu,Z) – возвращает функцию Бесселя первого рода, J _v (z), для каждого элемента комплексного массива Z. Порядок ш может не быть целым, однако должен быть вещественным. Аргумент Z может быть комплексным. Результат вещественный, если Z положительно. Если nu и Z – массивы одинакового размера, то результат имеет тот же размер. Если любая входная величина – скаляр, результат расширяется до размера другой входной величины. Если одна входная величина – вектор-строка, а другая – вектор-столбец, результат представляет собой двумерный массив значений функции.
• bessely(nu.Z) – возвращает функцию Бесселя второго рода, Y_v (z).
• [J.ierr] = besselj(nu,Z) и [Y.ierr] = bessely(nu.Z) функции всегда возвращают массив с флагами ошибок:
  • ierr = 1 – запрещенные аргументы;
  • ierr = 2 – переполнение (возвращает Inf);
  • ierr = 3 – некоторая потеря точности при приведении аргумента;
  • ierr = 4 – недопустимая потеря точности: Z или nu слишком велики;
  • ierr = 5 – нет сходимости (возвращает NaN).

Примеры:

• besselh(nu,К,Z) – для К=1 или 2 возвращает функцию Бесселя третьего рода (функцию Ханкеля) для каждого элемента комплексного массива Z. Если nu и Z – массивы одинакового размера, то результат имеет тот же размер. Если одна из входных величин – скаляр, результат формируется по размеру другой входной величины. Если одна входная величина – вектор-строка, а другая – вектор-столбец, результат представляет собой двумерный массив значений функции.
• besselh(nu.Z) – использует по умолчанию К = 1.
• besselh(nu.l.Z.l) – масштабирует H⁽¹⁾ _v (z) с коэффициентом exp(-i*z).
• besselh(nu,2,Z.l) – масштабирует H⁽²⁾ _v (z) с коэффициентом exp(+i*z).
• [H.ierr] = besselh(…) – всегда возвращает массив с флагами ошибок:
  • ierr = 1 – запрещенные аргументы;
  • ierr = 2 – переполнение (возвращает Inf);
  • ierr = 3 – некоторая потеря точности при приведении аргумента;
  • ierr = 4 – недопустимая потеря точности: Z или nu слишком велики;
  • ierr = 5 – нет сходимости (возвращает NaN).