Расширенная техника анимации
Анимирование разложения импульса в ряд Фурье
Анимирование изображений является одним из самых мощных средств визуализации результатов моделирования тех или иных зависимостей или явлений.
Порою изменение во времени одного из параметров зависимости дает наглядное представление о его математической или физической сути.
Здесь мы расширим представление об анимации и рассмотрим не вполне обычный пример – наблюдение в динамике за гармоническим синтезом некоторой произвольной функции f(x) на отрезке изменения n; от 0 до 1. Значения функции f(x) могут быть одного знака или разных знаков. В этом примере можно наблюдать в динамике синтез заданной функции рядом Фурье с ограниченным числом синусных членов (гармоник) – до 1, 2, 3..JV.
На рис. 12.50 представлен документ, реализующий такое разложение и затем синтез для пилообразного линейно нарастающего импульса, описываемого выражением f(x) = -1 + 2 *х. На графике строится исходная функция и результат ее синтеза в динамике анимации.
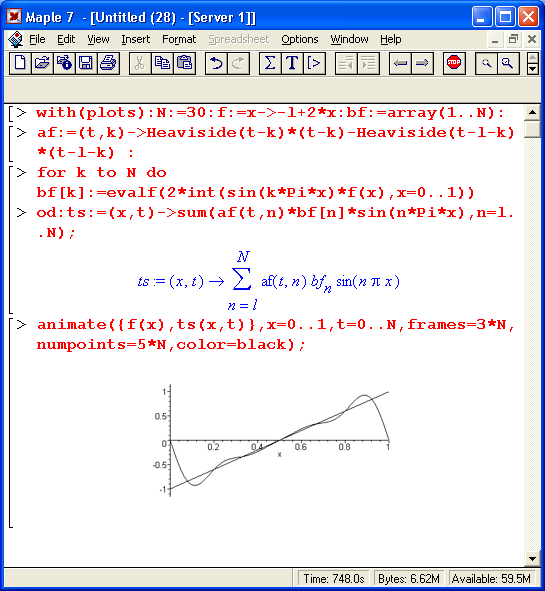
Рис. 12.50. Один из первых стоп-кадров анимации разложения импульса в ряд Фурье
Рисунок 12.51 показывает завершающий стоп-кадр анимации, когда число гармоник N равно 30. Нетрудно заметить, что такое число гармоник в целом неплохо описывает большую часть импульса, хотя в. его начале и в конце все еще заметны сильные отклонения.
Для f(x) = 1 строится приближение для однополярного импульса с длительностью 1 и амплитудой 1, при f(x) =х – приближение для пилообразного линейно нарастающего импульса, при f(x) =х^2 – приближение для нарастающего по параболе импульса, при f(x)=signum(x-1/2) – приближение для симметричного прямоугольного импульса-меандра и т. д.
