Иллюстрированный самоучитель по Maple 6/7

Иллюстрация итерационного решения уравнения f (х) = х

Классическим методом решения нелинейных уравнений является сведение их к виду х =f(x) и применение метода простых итераций x_k =s(x_k-1) при заданном значении х₀.

Приведем пример такого решения:

>f: = x › 3*1n(x+l);
f: = x › 3ln(x+1)
>x||0: = 0.5:
x0: = 5
>x0: =. 5;
x0: =. 5
>for k from 1 to 16 do x||k: = evalf(f(x||(k-l))): od;
x1: = 1.216395324
x2: = 2.387646445
x3: = 3.660406248
x4: = 4.617307866
x5: = 5.177557566
x6: = 5.462768931
x7: = 5.598173559
x8: = 5.660378631
x9: = 5.688529002
x10: = 5.701181910
x11: = 5.706851745
x12: = 5.709388956
x13: = 5.710523646
x14: = 5.711030964
xl5: = 5.711257755
x16: = 5.711359134

Нетрудно заметить, что значения x_k в ходе итераций явно сходятся к некоторому значению. Проведем проверку решения, используя встроенную функцию solve:

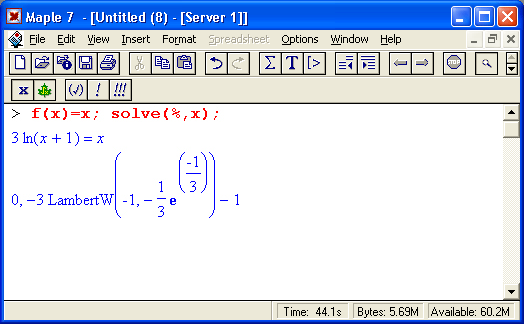
Результат выглядит необычно – помимо довольно "очевидного" корня х x= 0 значение другого корня получено в виде специальной функции Ламберта. Впрочем, нетрудно найти и его численное значение:

> evalf(%);
0., 5.711441084

Однако как сделать процесс решения достаточно наглядным? Обычно для этого строят графики двух зависимостей – прямой х и кривой f(x) – и наносят на них ступенчатую линию перемещения точки x_k.