Системы уравнений
Графическая интерпретация рассмотренной системы представлена на рис. 8.3. Каждое из уравнений показано на плоскости XY графиком. Первое – сплошной кривой, второе – пунктиром. Поскольку второе уравнение линейное, то оно определяет на плоскости XY прямую. Две точки пересечения кривых соответствуют одновременному выполнению обоих уравнений, т. е. искомым действительным корням системы. Как нетрудно убедиться, в листинге найдено только одно из двух решений – находящееся в правой нижней части графика. Чтобы отыскать и второе решение, следует повторить вычисления, изменив начальные значения так, чтобы они лежали ближе к другой точке пересечения графиков, например x=-1, y=-1.
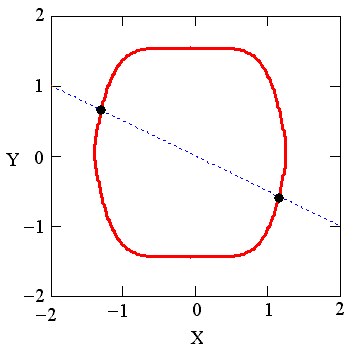
Рис. 8.3. Графическое решение системы двух уравнений
Пока мы рассмотрели пример системы из двух уравнений и таким же числом неизвестных, что встречается наиболее часто. Но число уравнений и неизвестных может и не совпадать. Более того, в вычислительный блок можно добавить дополнительные условия в виде неравенств. Например, введение ограничения на поиск только отрицательных значений х в рассмотренный выше листинг 8.6 приведет к нахождению другого решения, как это показано в листинге 8.7.
Листинг 8.7. Решение системы уравнений и неравенств:
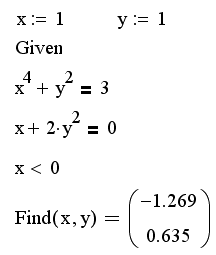
Обратите внимание, что, несмотря на те же начальные значения, что и в листинге 8.6, мы получили в листинге 8.7 другой корень. Это произошло именно благодаря введению дополнительного неравенства, которое определено в блоке Given в предпоследней строке листинга 8.7.
Если предпринять попытку решить несовместную систему, Mathcad выдаст сообщение об ошибке, гласящее, что ни одного решения не найдено, и предложение попробовать поменять начальные значения или значение погрешности.
Вычислительный блок использует константу CTOL в качестве погрешности выполнения уравнений, введенных после ключевого слова Given. Например, если CTOL=0.001, то уравнение х=10 будет считаться выполненным и при х=10.001, и при х=9.999. Другая константа TOL определяет условие прекращения итераций численным алгоритмом (см. разд. 8.4). Значение CTOL может быть задано пользователем так же как и TOL, например, CTOL: = 0.01. По умолчанию принято, что CTOL=TOL=0.001, но Вы по желанию можете переопределить их.
Особенную осторожность следует соблюдать при решении систем с числом неизвестных большим, чем число уравнений. Например, можно удалить одно из двух уравнений из рассмотренного нами листинга 8.6, попытавшись решить единственное уравнение g(х,у)=о с двумя неизвестными х и у. В такой постановке задача имеет бесконечное множество корней: для любого х и, соответственно, у=-х/2 условие, определяющее единственное уравнение, выполнено. Однако, даже если корней бесконечно много, численный метод будет производить расчеты только до тех пор, пока логические выражения в вычислительном блоке не будут выполнены (в пределах погрешности). После этого итерации будут остановлены и выдано решение. В результате будет найдена всего одна пара значений (х,у), обнаруженная первой.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
О том, как найти все решения рассматриваемой задачи, рассказывается в разд. 8.7.
Вычислительным блоком с функцией Find можно найти и корень уравнения с одним неизвестным. Действие Find в этом случае совершенно аналогично уже рассмотренным в данном разделе примерам. Задача поиска корня рассматривается как решение системы, состоящей из одного уравнения. Единственным отличием будет скалярный, а не векторный тип числа, возвращаемого функцией Find. Пример решения уравнения из предыдущего раздела приведен в листинге 8.8.
Листинг 8.8. Поиск корня уравнения с одним неизвестным с помощью функции Find:
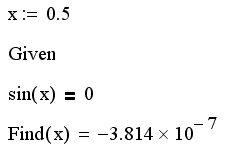
В чем же отличие приведенного решения от листинга 8.1 с функцией root? Оно состоит в том, что одна и та же задача решена различными численными методами. В данном случае выбор метода не влияет на окончательный результат, но бывают ситуации, когда применение того или иного метода имеет решающее значение.
