Одно уравнение с одним неизвестным
Рассмотрим одно алгебраическое уравнение с одним неизвестным х.
f(x) = 0, (1)Например, sin(x)=0.
Для решения таких уравнений Mathcad имеет встроенную функцию root, которая, в зависимости от типа задачи, может включать либо два, либо четыре аргумента и, соответственно, работает несколько по-разному.
- root(f(х),х);
- root(f(х),х,а,b);
- f (х) – скалярная функция, определяющая уравнение (1);
- х – скалярная переменная, относительно которой решается уравнение;
- a,b – границы интервала, внутри которого происходит поиск корня.
Первый тип функции root требует дополнительного задания начального значения (guess value) переменной х. Для этого нужно просто предварительно присвоить х некоторое число. Поиск корня будет производиться вблизи этого числа. Таким образом, присвоение начального значения требует априорной информации о примерной локализации корня.
Приведем пример решения очень простого уравнения sin(x)=0, корни которого известны заранее.
Листинг 8.1. Поиск корня нелинейного алгебраического уравнения:
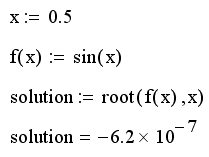
График функции f (x)=sin(x) и положение найденного корня показаны на рис. 8.1.
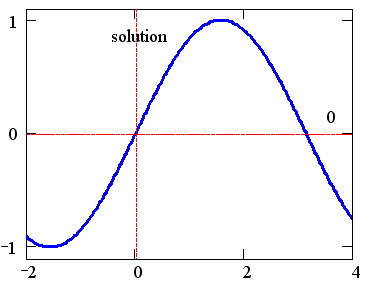
Рис. 8.1. Графическое решение уравнения sin(x)=0
Обратите внимание, что, хотя уравнение имеет бесконечное количество корней xn=npi (n=0,±1,±2,…), Mathcad находит (с заданной точностью) только один из них, х0, лежащий наиболее близко к х=0.5. Если задать другое начальное значение, например х=3, то решением будет другой корень уравнения х1=pi и т. д. Таким образом, для поиска корня средствами Mathcad требуется его предварительная локализация. Это связано с особенностями выбранного численного метода, который называется методом секущих и состоит в следующем (рис. 8.2):
- Начальное приближение принимается за 0-е приближение к корню: х0=х.
- Выбирается шаг h=TOLх и определяется первое приближение к корню x1=x0+h. Если х=0, то принимается h=TOL.
- Через эти две точки проводится секущая – прямая линия, которая пересекает ось х в некоторой точке х2. Эта точка принимается за второе приближение.
- Новая секущая проводится через первую и вторую точки, тем самым определяя третье приближение, и т. д.
- Если на каком-либо шаге оказывается, что уравнение выполнено, т. е. |If (x) |<TOL, то итерационный процесс прерывается, и х выдается в качестве решения.
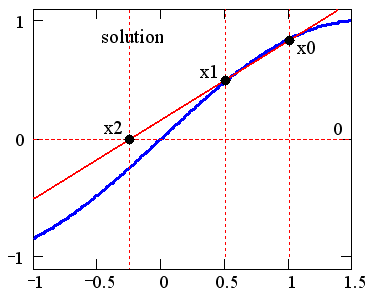
Рис. 8.2. Иллюстрация метода секущих
Результат, показанный на рис. 8.2, получен для погрешности вычислений, которой в целях иллюстративности предварительно присвоено значение TOL=0.5. Поэтому для поиска корня с такой невысокой точностью оказалось достаточно одной итерации. В вычислениях, приведенных в листинге 8.1, погрешность TOL=0.001 была установлена по умолчанию, и решение, выданное численным методом, лежало намного ближе к истинному положению корня х=0. Иными словами, чем меньше константа TOL, тем ближе к нулю будет значение f (x) в найденном корне, но тем больше времени будет затрачено вычислительным процессором Mathcad на его поиск.
Соответствующий пример можно найти в Быстрых шпаргалках, на странице Ресурсов Mathcad. Он расположен в разделе "Solving Equations" (Решение уравнений) и называется "Effects of TOL on Solving Equations" (Влияние константы TOL на решение уравнений).
