Иллюстрированный самоучитель по MathCAD 11

Приближенное решение уравнений

Иногда приходится заменять задачу определения корней системы уравнений задачей поиска экстремума функции многих переменных. Например, когда невозможно найти решение с помощью функции Find, можно попытаться потребовать вместо точного выполнения уравнений условий минимизировать их невязку. Для этого следует в вычислительном блоке вместо функции Find использовать функцию Minerr, имеющую тот же самый набор параметров. Она также должна находиться в пределах вычислительного блока:

• x₁: = C₁… х_м: =C_м – начальные значения для неизвестных.
• Given – ключевое слово.
• Система алгебраических уравнений и неравенств, записанная логическими операторами.
• Minerr (x₁,…,х_м) – приближенное решение системы относительно переменных х₁;…,х_м, минимизирующее невязку системы уравнений.

В функции Minerr реализованы те же самые алгоритмы, что и в функции Find, иным является только условие завершения работы численного метода. Поэтому пользователь может тем же самым образом, с помощью контекстного меню (см. разд. 8.4), выбирать численный алгоритм приближенного решения для функции Minerr.

Пример использования функции Minerr показан в листинге 8.9. Как видно, достаточно заменить в вычислительном блоке имя функции на Minerr, чтобы вместо точного (с точностью до TOL) получить приближенное решение уравнения, заданного после ключевого слова Given.

Листинг 8.9. Приближений решение уравнения, имеющего корень (x=0, y=0):

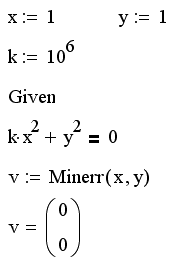
Листинг 8.9 демонстрирует приближенное решение уравнения kx² +y²: = 0, которое при любом значении коэффициента k имеет единственный точный корень (х=0,у=0). Тем не менее, при попытке решить его функцией Find для больших k, порядка принятых в листинге, происходит генерация ошибки "No solution was found" (Решение не найдено). Это связано с иным поведением функции f (x,y)=kx² +y² вблизи ее корня, по сравнению с функциями, приводимыми в качестве примеров выше в этой главе (см. рис. 8.1, 8.2). В отличие от них, f (х,у) не пересекает плоскость f (х,у)=о, а лишь касается ее (рис. 8.7) в точке (х=0,у=0). Поэтому и найти корень изложенными в предыдущем разделе градиентными методами сложнее, поскольку вблизи корня производные f (х,у) близки к нулю, и итерации могут уводить предполагаемое решение далеко от корня.

Ситуация еще более ухудшается, если наряду с корнем типа касания (см. рис. 8.7) имеются (возможно, весьма удаленные) корни типа пересечения. Тогда попытка решить уравнение или систему уравнений с помощью функции Find может приводить к нахождению корня второго типа, даже если начальное приближение было взято очень близко к первому. Поэтому если Вы предполагаете, что система уравнений имеет корень типа касания, намного предпочтительнее использовать функцию Minerr, тем более, что всегда есть возможность проверить правильность решения уравнений простой подстановкой в них полученного решения (см. листинг 8.6).

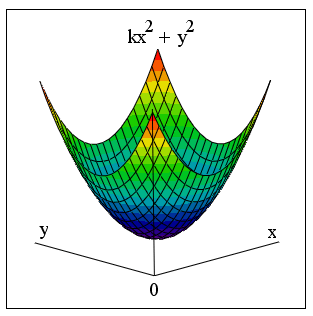
Рис. 8.7. График функции kx² +y²

В листинге 8.9 мы рассмотрели пример нахождения существующего решения уравнения. Приведем в заключение пример нахождения функцией Minerr приближенного решения несовместной системы уравнений и неравенств (листинг 8.10). Решение, выдаваемое функцией Minerr, минимизирует невязку данной системы.

Согласно своему математическому смыслу, функция Minerr может применяться для построения регрессии серии данных по закону, заданному пользователем (см. разд. 15.2).

Листинг 8.10. Приближенное решение несовместной системы уравнений и неравенств:

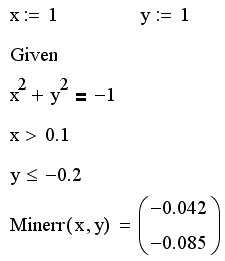
Как видно из листинга, в качестве результата выдаются значения переменных, наилучшим образом удовлетворяющие уравнению и неравенствам внутри вычислительного блока. Внимательный читатель может обнаружить, что решение, выдаваемое функцией Minerr в рассматриваемом примере, не является единственным, поскольку множество пар значений (х,у) в равной степени минимизирует невязку данной системы уравнений и неравенств. Поэтому для различных начальных значений будут получаться разные решения, подобно тому как разные решения выдаются функцией Find в случае бесконечного множества корней (см. обсуждение листинга 8.6 в разд. 8.3).

Еще более опасен случай, когда имеются всего несколько локальных минимумов функции невязки. Тогда неудачно выбранное начальное приближение приведет к выдаче именно этого локального минимума, несмотря на то, что другой (глобальный) минимум невязки может удовлетворять системе гораздо лучше.