Системы уравнений
Рассмотрим решение системы N нелинейных уравнений с M неизвестными:
- f1(x1,…,хм) = 0,
- … (1)
- fn(x1,…,хм) = 0,
Здесь f1(x1,…,хм),…, fn(x1, …,хм) – некоторые скалярные функции от скалярных переменных хмх2/ … /хм и, возможно, от еще каких-либо переменных. Уравнений может быть как больше, так и меньше числа переменных. Заметим, что систему (1) можно формально переписать в виде:
f(x) = 0, (2)Где х – вектор, составленный из переменных x1,х2,…,хм, a f (х) – соответствующая векторная функция.
Для решения систем имеется специальный вычислительный блок, состоящий из трех частей, идущих последовательно друг за другом:
- Given – ключевое слово;
- система, записанная логическими операторами в виде равенств и, возможно, неравенств;
- Find(x1…,хм) – встроенная функция для решения системы относительно переменных хх,…, хм.
Вставлять логические операторы следует, пользуясь панелью инструментов Boolean (Булевы операторы). Если Вы предпочитаете ввод с клавиатуры, помните, что логический знак равенства вводится сочетанием клавиш CTRL + =. Блок Given/Find использует для поиска решения итерационные методы, поэтому, как и для функции root, требуется задать начальные значения для всех х1,…, xм. Сделать это необходимо до ключевого слова Given. Значение функции Find есть вектор, составленный из решения пс каждой переменной. Таким образом, число элементов вектора равно число аргументов Find.
В листинге 8.6. приведен пример решения системы двух уравнений.
Листинг 8.6. Решение системы уравнений:
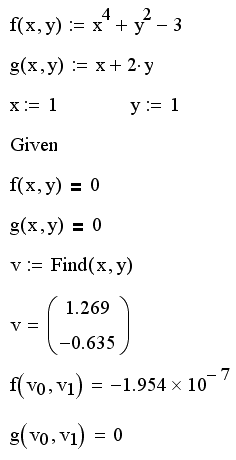
В первых двух строках листинга вводятся функции, которые определяют систему уравнений. Затем переменным х и у, относительно которых она будет решаться, присваиваются начальные значения. После этого следует ключевое слово Given и два логических оператора, выражающих рассматриваемую систему уравнений. Завершает вычислительный блок функция Find, значение которой присваивается вектору v. Следующая строка показывает содержание вектора v, т. е. решение системы. Первый элемент вектора есть первый аргумент функции Find, второй элемент – ее второй аргумент. В последних двух строках осуществлена проверка правильности решения уравнений.
Часто бывает очень полезно проверить точность решения уравнений, вычислив значения образующих их функций в найденных вычислительным процессором корнях, как это сделано в конце листинга 8.6.
Отметим, что уравнения можно определить непосредственно внутри вычислительного блока. Таким образом, можно не определять заранее функции f (x,y) и g(х,у), как это сделано в первых двух строках листинга 8.6, а сразу написать:
- Given
- х4 + у2 =3
- х+ 2 у = 0
Такая форма представляет уравнения в более привычной и наглядной форме, особенно подходящей для документирования работы.