Иллюстрированный самоучитель по MathCAD 11

Линейное программирование

Задачи поиска условного экстремума функции многих переменных часто встречаются в экономических расчетах для минимизации издержек, финансовых рисков, максимизации прибыли и т. п. Целый класс экономических задач оптимизации описывается системами линейных уравнений и неравенств. Они называются задачами линейного программирования.

Приведем характерный пример т. н. транспортной задачи, которая решает одну из проблем оптимальной организации доставки товара потребителям с точки зрения экономии транспортных средств (листинг 8.15).

Листинг 8.15. Решение задачи линейного программирования:

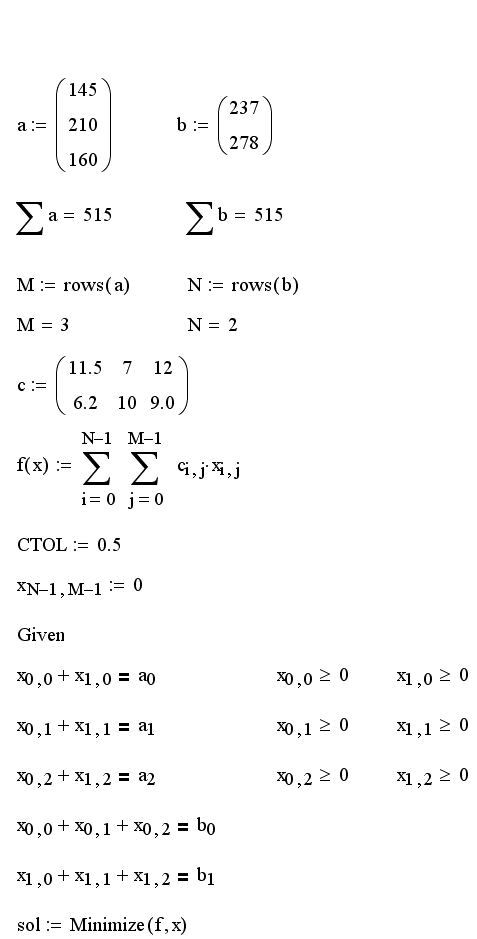
Модель типичной транспортной задачи следующая. Пусть имеется N предприятий-производителей, выпустивших продукцию в количестве b₀,…,b_n-1, тонн. Эту продукцию требуется доставить м потребителям в количестве a₀,…, a_м-1 тонн каждому. Численное определение векторов а и b находится в первой строке листинга. Сумма всех заказов потребителей a_i равна сумме произведенной продукции, т. е. всех b_i (проверка равенства во второй строке). Если известна стоимость перевозки тонны продукции от 1-го производителя к j-му потребителю c_ij то решение задачи задает оптимальное распределение соответствующего товаропотока x_ij с точки зрения минимизации суммы транспортных расходов. Матрица с и минимизируемая функция f (х) матричного аргумента х находятся в середине листинга 8.15.

Условия, выражающие неотрицательность товаропотока, и равенства, задающие сумму произведенной каждым предприятием продукции и сумму заказов каждого потребителя, находятся после ключевого слова Given. Решение, присвоенное матричной переменной sol, выведено в последней строке листинга вместе с соответствующей суммой затрат. Обратите внимание, что для получения результата пришлось увеличить погрешность CTOL, задающую максимальную допустимую невязку дополнительных условий. В строке, предшествующей ключевому слову Given, определяются нулевые начальные значения для x простым созданием нулевого элемента матрицы x_{n-1, м-1}.

Если взять другие начальные значения для х, решение, скорее всего, будет другим! Возможно, Вы сумеете отыскать другой локальный минимум, который еще больше минимизирует транспортные затраты. Это еще раз доказывает, что задачи на глобальный минимум, к классу которых относится линейное программирование, требуют аккуратного отношения в смысле выбора начальных значений. Часто ничего другого не остается, кроме сканирования всей области начальных значений, чтобы из множества локальных минимумов выбрать наиболее глубокий.