Разностные схемы для ОДУ. О разностном методе решения ОДУ.
Многие краевые задачи не поддаются решению методом стрельбы. Однако в Mathcad 11 других встроенных алгоритмов нет. Тем не менее, это не означает, что по-другому решать краевые задачи невозможно, ведь другие численные алгоритмы несложно запрограммировать самому пользователю. Рассмотрим возможную реализацию наглядного метода, называемого разностным, которым можно решать краевые задачи как для ОДУ, так и для дифференциальных уравнений в частных производных.
Разберем идею разностного метода решения краевых задач на примере взаимодействия световых пучков (см. рис. 12.1), переобозначив в системе (12.1.1) интенсивность излучения вправо на Y, а интенсивность излучения влево на у (просто в целях удобства, чтобы не писать индекс). Суть метода заключается в покрытии расчетного интервала сеткой из N точек. Тем самым определяются (N-I) шагов (рис. 12.7). Затем надо заменить дифференциальные уравнения исходной краевой задачи аппроксимирующими их уравнениями в конечных разностях, выписав соответствующие разностные уравнения для каждого 1-го шага. В нашем случае достаточно просто заменить первые производные из (12.1.1) их разностными аналогами (такой метод называется еще методом Эйлера).
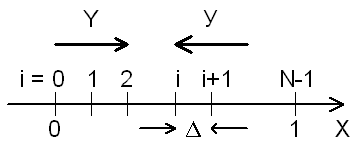
Рис. 12.7. Сетка, покрывающая расчетный интервал
Существует множество способов аппроксимации дифференциальных уравнений разностными. От выбора конкретного варианта зависит не только простота, быстрота и удобство вычислений, но и сама возможность получения правильного ответа.
Получилась система (по числу шагов) 2 (N-1) разностных линейных алгебраических уравнений с 2N неизвестными Yi и уi,.. Для того чтобы она имела единственное решение, надо дополнить число уравнений до 2N. Это можно сделать, записав в разностном виде оба граничных условия: Y0=I0, YN=RYN (2).
Сформированная полная система алгебраических уравнений называется разностной схемой, аппроксимирующей исходную краевую задачу. Обратите внимание, что правые части разностных уравнений системы (1) на каждом шаге записаны для левой границы шага. Такие разностные схемы называют явными, т. к. все значения Yi+1 и Y1+i находятся в левой части уравнений. Полученную явную разностную схему легко записать в матричной форме: Az=B, (3)
Где z – неизвестный вектор, получающийся объединением векторов Y и у. Решив систему (3), мы получим решение краевой задачи.
На самом деле, все несколько сложнее, поскольку, вообще говоря, необходимо еще доказать, что, во-первых, разностная схема действительно аппроксимирует дифференциальные уравнения и, во-вторых, при N разностное решение действительно сходится к дифференциальному.
Процесс решения системы разностных уравнений называют также реализацией разностной схемы. Программа, которая решает рассматриваемую краевую задачу разностным методом, приведена в листинге 12.6.
Листинг 12.6. Реализация явной разностной схемы:
