Разностные схемы для ОДУ. О разностном методе решения ОДУ.
Дадим минимальные комментарии, надеясь, что заинтересовавшийся читатель с карандашом в руках разберется в порядке индексов и соответствии матричных элементов, а возможно, составит и более удачную программу.
В первой строке листинга определяются функции и константы, входящие в модель, во второй задается число точек сетки N=5 и ее равномерный шаг. Следующие две строки определяют матричные коэффициенты, аппроксимирующие уравнения для уi а пятая и шестая – для ух. Седьмая и восьмая строки листинга задают, соответственно, левое и правое граничное условие, а строки с девятой по одиннадцатую – правые части системы (3). В следующей строке завершается построение матрицы А вырезанием из нее левого нулевого столбца. В предпоследней строке листинга применена встроенная функция isolve для решения системы (3), а в последней выведены рассчитанные ею неизвестные граничные значения. Графики решения приведены на рис. 12.8, причем первые N элементов итогового вектора есть вычисленное излучение вперед, а последние N элементов – излучение назад.
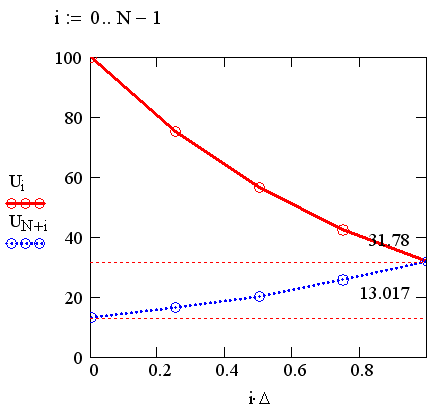
Рис. 12.8. Решение краевой задачи разностным методом (листинг 12.6)
Как мы увидели, реализация в Mathcad разностных схем вполне возможна и не слишком трудоемка – предложенная программа состоит всего из двух десятков математических выражений. Конечно, для их написания требуется и время, и часто кропотливые расчеты, но, собственно, в этом и состоит работа математика. Кстати говоря, при небольшом числе шагов, расчеты по разностным схемам не требуют существенного времени (программа, приведенная в листинге 12.6, работает быстрее, чем метод стрельбы, встроенный в функцию sbval). Существуют, кроме того, весьма очевидные для многих читателей пути ускорения расчетов, связанные с применением более подходящих методов решения систем линейных уравнений с разреженной матрицей.
