Интегральные преобразования. Преобразование Фурье.
Преобразование Фурье комплексных данных
Алгоритм быстрого преобразования Фурье для комплексных данных встроен в соответствующие функции, в имя которых входит литера "с".
- cfft(y) – вектор прямого комплексного преобразования Фурье;
- CFFT(y) – вектор прямого комплексного преобразования Фурье в другой нормировке;
- icfft(y) – вектор обратного комплексного преобразования Фурье;
- ICFFT(V) – вектор обратного комплексного преобразования Фурье в другой нормировке;
- у – вектор данных, взятых через равные промежутки значений аргумента;
- v – вектор данных Фурье-спектра, взятых через равные промежутки значений частоты.
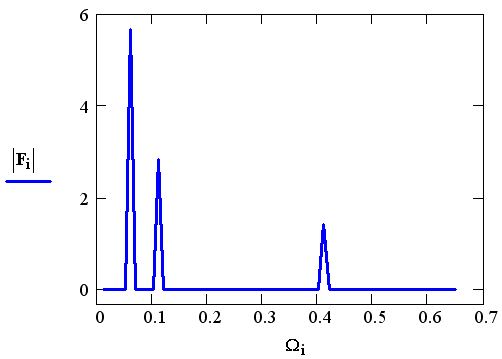
Рис. 15.25. Преобразование Фурье (листинг 15.20)
Функции действительного преобразования Фурье используют тот факт, что в случае действительных данных спектр получается симметричным относительно нуля, и выводят только его половину (см. выше разд. "Преобразование Фурье действительных данных" этой главы). Поэтому, в частности, по 128 действительным данным получалось всего 65 точек спектра Фурье. Если к тем же данным применить функцию комплексного преобразования Фурье (рис. 15.26), то получится вектор из 128 элементов. Сравнивая рис. 15.25 и 15.26, можно уяснить соответствие между результатами действительного и комплексного Фурье-преобразования.
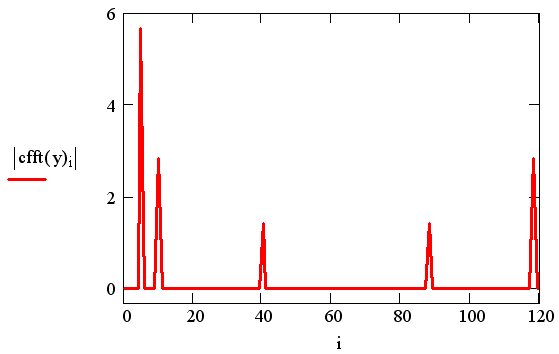
Рис. 15.26. Комплексное преобразование Фурье (продолжение листинга 15.20)
Двумерное преобразование Фурье
В Mathcad имеется возможность применять встроенные функции комплексного преобразования Фурье не только к одномерным, но и к двумерным массивам, т. е. матрицам. Соответствующий пример приведен в листинге 15.21 и на рис. 15.27 в виде графика линий уровня исходных данных и рассчитанного Фурье-спектра.
Листинг 15.21. Двумерное преобразование Фурье:

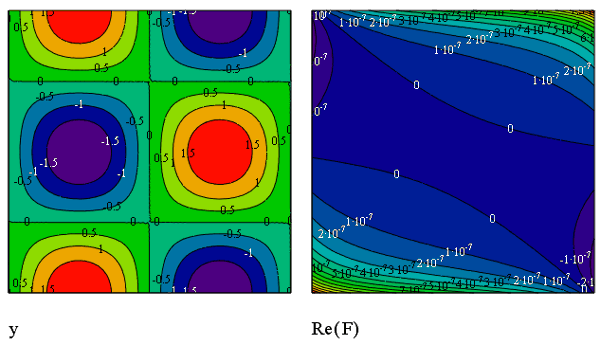
Рис. 15.27. Данные (слева) и их Фурье-спектр (справа) (листинг 15.21)
