Линейная интерполяция
Самый простой вид интерполяции – линейная, которая представляет искомую зависимость А(Х) в виде ломаной линии. Интерполирующая функция А(Х) состоит из отрезков прямых, соединяющих точки (рис. 15.2).
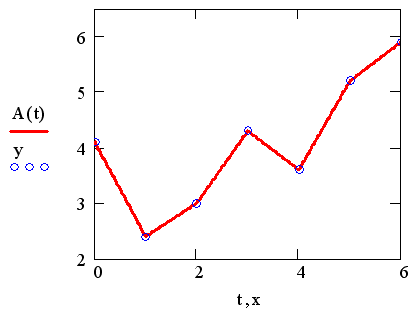
Рис. 15.2. Линейная интерполяция (листинг 15.1)
Для построения линейной интерполяции служит встроенная функция linterp (листинг 15.1).
- linterp(x, y, t) – функция, аппроксимирующая данные векторов х и у кусочно-линейной зависимостью;
- х – вектор действительных данных аргумента;
- у – вектор действительных данных значений того же размера;
- t – значение аргумента, при котором вычисляется интерполирующая функция.
Элементы вектора х должны быть определены в порядке возрастания, т. е. Х1<Х2<Х3< … <Xn.
Листинг 15.1. Линейная интерполяция:
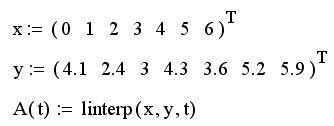
Как видно из листинга, чтобы осуществить линейную интерполяцию, надо выполнить следующие действия:
- Введите векторы данных х и у (первые две строки листинга).
- Определите функцию linterp(х,у, t).
- Вычислите значения этой функции в требуемых точках, например lin-terp(x,y, 2.4)=3.52 или iinterp(x,y,6) =5.9, или постройте ее график, как показано на рис. 15.2.
Обратите внимание, что функция A(t) на графике имеет аргумент t, а не х. Это означает, что функция А (с) вычисляется не только при значениях аргумента (т. е. в семи точках), а при гораздо большем числе аргументов в интервале (0.6), что автоматически обеспечивает Mathcad. Просто в данном случае эти различия незаметны, т. к. при обычном построении графика функции А(х) от векторного аргумента х (рис. 15.3) Mathcad, по умолчанию, соединяет точки графика прямыми линиями (т. е. скрытым образом осуществляет их линейную интерполяцию).
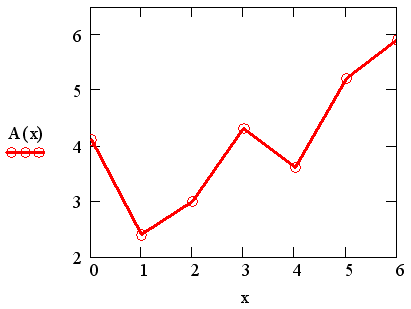
Рис. 15.3. Обычное построение графика функции от векторной переменной х (листинг 15.1)
