Скользящее усреднение
Помимо встроенных в Mathcad, существует несколько популярных алгоритмов сглаживания, на одном из которых хочется остановиться особо. Самый простой и очень эффективный метод – это скользящее усреднение. Его суть состоит в расчете для каждого значения аргумента среднего значения по соседним w данным. Число w называют окном скользящего усреднения; чем оно больше, тем больше данных участвуют в расчете среднего, тем более сглаженная кривая получается.
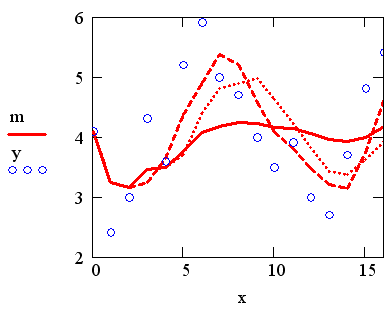
Рис. 15.21. Скользящее усреднение с разными w=3.5.15 (листинг 15.17, коллаж трех графиков)
На рис. 15.21 показан результат скользящего усреднения одних и тех же данных (кружки) с разным окном w=3 (пунктир), w=5 (штрихованная кривая) и w=is (сплошная кривая). Видно, что при малых w сглаженные кривые практически повторяют ход изменения данных, а при больших w – отражают лишь закономерность их медленных вариаций.
Чтобы реализовать в Mathcad скользящее усреднение, достаточно очень простой программы, приведенной в листинге 15.17. Она использует только значения у, оформленные в виде вектора, неявно предполагая, что они соответствуют значениям аргумента х, расположенным через одинаковые промежутки. Вектор х применялся лишь для построения графика результата (рис 15.21).
Листинг 15.17. Сглаживание скользящим усреднением:
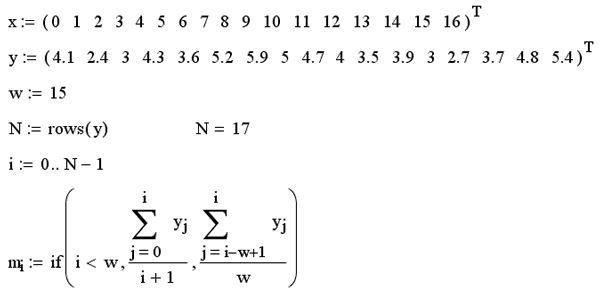
Приведенная программная реализация скользящего усреднения самая простая, но не самая лучшая. Возможно Вы обратили внимание, что все кривые скользящего среднего на рис 15.21 слегка "обгоняют" исходные данные. Почему так происходит, понятно согласно алгоритму, заложенному в последнюю строку листинга 15.17, скользящее среднее для каждой точки вычисляется путем усреднения значений предыдущих w точек. Чтобы результат скользящего усреднения был более адекватным лучше применить центрированный алгоритм расчета по w/2 предыдущим и w/2 последующим значениям. Он будет немного сложнее, поскольку придется учитывать недостаток точек не только в начале (как это сделано в программе с помощью функции условия if) но и в конце массива исходных данных.
