MATLAB в роли суперкалькулятора. О переносе строки в сессии.
Система MATLAB создана таким образом, что любые (подчас весьма сложные) вычисления можно выполнять в режиме прямых вычислений, то есть без подготовки программы. Это превращает MATLAB в необычайно мощный калькулятор, который способен производить не только обычные для калькуляторов вычисления (например, выполнять арифметические операции и вычислять элементарные функции), но и операции с векторами и матрицами, комплексными числами, рядами и полиномами. Можно почти мгновенно задать и вывести графики различных функций – от простой синусоиды до сложной трехмерной фигуры.
Работа с системой в режиме прямых вычислений носит диалоговый характер и происходит по правилу "задал вопрос, получил ответ". Пользователь набирает на клавиатуре вычисляемое выражение, редактирует его (если нужно) в командной строке и завершает ввод нажатием клавиши ENTER. В качестве примера на рис. 2.9 уже были показаны простейшие вычисления – вычисление выражения 2+3 и значения sin(l).
Даже из таких простых примеров можно сделать некоторые поучительные выводы:
- для указания ввода исходных данных используется символ ";
- данные вводятся с помощью простейшего строчного редактора;
- для блокировки вывода результата вычислений некоторого выражения после него надо установить знак ; (точка с запятой);
- если не указана переменная для значения результата вычислений, то MATLAB назначает такую переменную с именем ans;
- знаком присваивания является привычный математикам знак равенства =, а не комбинированный знак :=, как во многих других языках программирования и математических системах;
- результат вычислений выводится в строках вывода (без знака >>);
- встроенные функции (например, sin) записываются строчными буквами, и их аргументы указываются в круглых скобках;
- диалог происходит в стиле "задал вопрос – получил ответ".
Следующий пример (он показан на рис. 2.11) иллюстрирует применение системы MATLAB для выполнения простых векторных операций. В этом примере задается четырехэлементный вектор V со значениями элементов 1, 2, 3 и 4. Далее (сосредоточьте на этом внимание!) вычисляются функции синуса и экспоненты с аргументом в виде вектора, а не скаляра.
Две записи для вектора – V=[1 2 3 4] и V=[1.2.3.4] – являются идентичными. Таким образом, векторы задаются списком своих элементов, разделяемых пробелами или запятыми. Список заключается в квадратные скобки. Для выделения n-го элемента вектора V используется выражение V(n). Оно задает соответствующую индексированную переменную.
В большинстве математических систем вычисление sin(V) и exp(V), где V – вектор, сопровождалось бы выдачей ошибки, поскольку функции sin и ехр должны иметь аргумент в виде скалярной величины. Однако MATLAB – матричная система, а вектор является разновидностью матрицы с размером 1хn. Поэтому в нашем случае результат вычислений будет вектором того же размера, что и аргумент V, но элементы возвращаемого вектора будут синусами или экспонентами от элементов вектора V.
Еще один пример (рис. 2.12) демонстрирует простейшие операции с матрицей. Здесь задана матрица М с размером 2x2 и вычислена матрица MX=sin(M).
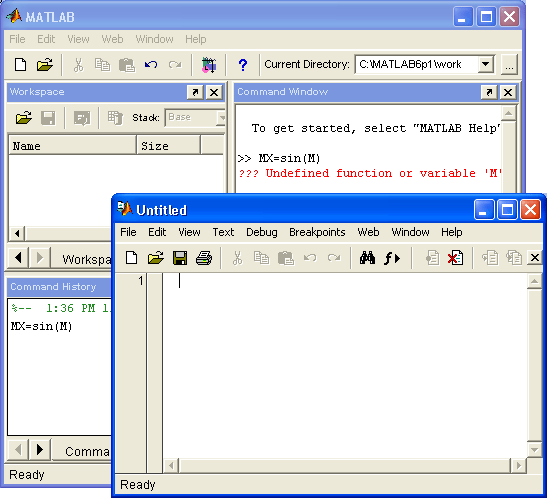
Рис. 2.12. Простейшие операции с матрицей
