Иллюстрированный самоучитель по Maple 6/7

Математические функции

Графики ряда алгебраических функций показаны на рис. 6.3.

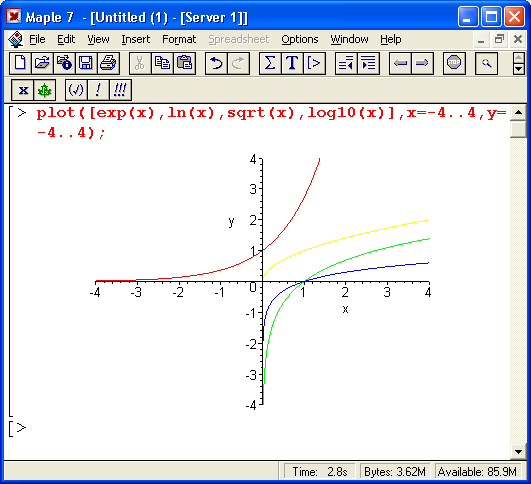
Рис. 6.3. Графики ряда алгебраических функций

На рис. 6.3 показаны также графики синусоиды с экспоненциально падающей и нарастающей амплитудой. Читателю рекомендуется попробовать свои силы в построении графиков комбинаций различных функций.

Функции с элементами сравнения

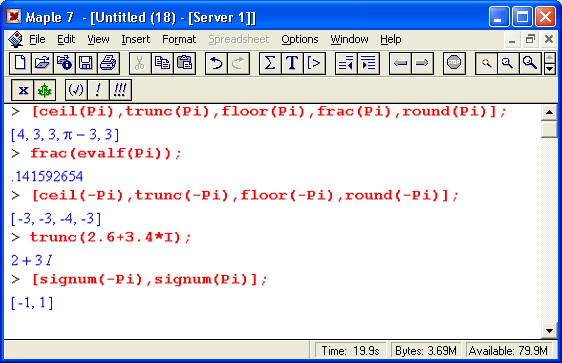
В алгоритме вычисления ряда функций заложено сравнение результата с некоторым опорным значением. К таким функциям относятся:

• abs – абсолютное значение числа;
• ceil – наименьшее целое, большее или равное аргументу;
• floor – наибольшее целое, меньшее или равное аргументу;
• frac – дробная часть числа;
• trunc – целое, округленное в направлении нуля;
• round – округленное значение числа;
• signum (х) – знак х (-1 при х < 0, 0 при х = 0 и +1 при х > 0).

Для комплексного аргумента х эти функции определяются следующим образом:

• tranc(x) = trunc(Re(*)) + I*trunc(IM(x));
• round(x) = round(Re(.r)) + I*round(Im(x));
• frac(x) -frac(Re(*)) + I*hac(Im(x)).

Для введения определения значения floor(x) от комплексного аргумента прежде всего запишем а = Re(x) -fооr(Re(x)) и b = Im(x) -floor(Im(x)). Тогда flооr(x) = floor(Re(x)) + I*floor(Im(x)) + X, где:

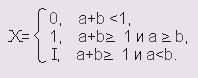
Наконец, функция ceil для комплексного аргумента определяется следующим образом:

Примеры применения: