Специальные математические функции
Специальные математические функции обычно являются решениями линейных дифференциальных уравнений различного типа и выражаются в виде интегралов, не представимых через элементарные функции. Maple 7 имеет практически полный набор таких функций. Их представления можно найти в справочной литературе, а также в справочной базе данных Maple. В связи с этим ограничимся приведением названий наиболее важных специальных функций:
- AiryAi (Bi) – функции Эйри;
- AngerJ – функция Ангера;
- bernoulli – числа и полиномы Бернулли;
- Bessel I (J, К, Y) – функции Бесселя разного рода;
- Beta – бета-функция;
- binomial – биноминальные коэффициенты;
- Chi – интегральный гиперболический косинус;
- Ci – интегральный косинус;
- csgn – комплексная сигнум-функция;
- dilog – дйлогарифм;
- Dirac – дельта-функция Дирака;
- Ei – экспоненциальный интеграл;
- EllipticCE (CK, CPi, E, F, К, Modulus, Nome, Pi) – эллиптические интегралы;
- erf – функция ошибок;
- erfc – дополнительная функция ошибок;
- euler – числа и полиномы Эйлера;
- FresnelC (f, g, S) – интегралы Френеля;
- GAMMA – гамма-функция;
- GaussAGM – арифметико-геометрическое среднее Гаусса;
- HankelHl (H2) – функции Ганкеля;
- harmonic – частичная сумма серии гармоник;
- Heaviside – функция Хевисайда;
- JacobiAM (CN, CD, CS, ON, DC, DS, NC, NO, NS, SC, SO, SN) – эллиптические функции Якоби;
- JacobiThetal (2, 3, 4) – дзета-функции Якоби;
- JacobiZeta – зет-функция Якоби;
- KelvinBer (Bei, Her, Hei, Ker, Kei) – функции Кельвина;
- Li – логарифмический интеграл;
- lnGAMMA – логарифмическая гамма-функция;
- MeijerG – G-функция Мейджера;
- pochhammer – символ Похгамера;
- polylog – полилогарифмическая функция;
- Psi – дигамма-функция;
- Shi – интегральный гиперболический синус;
- Si – интегральный синус;
- Ssi – синусный интеграл смещения;
- StruveH (L) – функции Струве;
- surd – неглавная корневая функция;
- LambertW – W-функция Ламберта;
- WeberE – Е-функция Вебера;
- WeierstrassP – Р-функция Вейерштрасса;
- WeierstrassPPrime – производная Р-функции Вейерштрасса;
- WeierstrassZeta – зета-функция Вейерштрасса;
- WeierstrassSigma – сигма-функция Вейерштрасса;
- Zeta – зета-функция Римана и Гурвица.
Ввиду большого числа специальных функций и наличия множества примеров их вычисления в справочной системе Maple 7 ограничимся несколькими примерами вычисления наиболее распространенных специальных функций. По их подобию читатель может опробовать в работе и другие специальные функции.
На рис. 6.4 даны примеры применения ряда специальных функций. Обратите особое внимание на первый пример. Он показывает, как средствами системы Maple 7 задается определение функций Бесселя. Показано, что функции Бесселя являются решениями заданного на рис. 6.4 дифференциального уравнения второго порядка. Maple 7 способна вычислять производные и интегралы от специальных функций.
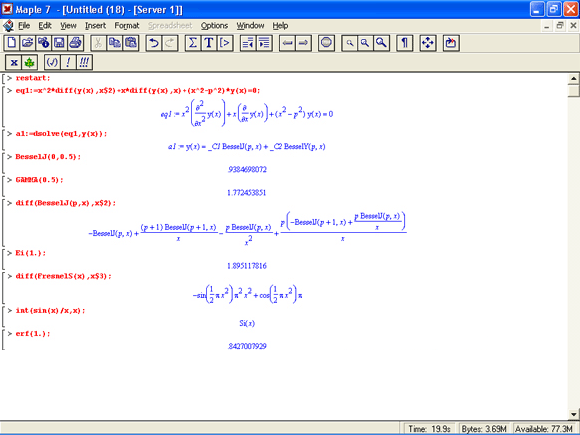
Рис. 6.4. Примеры применения специальных функций
