Разложение функций в ряды
Пример документа – разложение синуса в ряд
Полезно сочетать разложение выражений (функций) в ряд Тейлора с графической визуализацией такого разложения. Рассмотрим документ, в котором наглядно показаны возможности представления функции рядами Тейлора и Маклорена. На рис. 8.8 показана первая часть документа. Она дает пример разложения в ряд Тейлора функции sin(x) с построением ее графика и графика по разложению в ряд. Поскольку выбрано разложение относительно точки х = 0, то полученный ряд является рядом Маклорена.
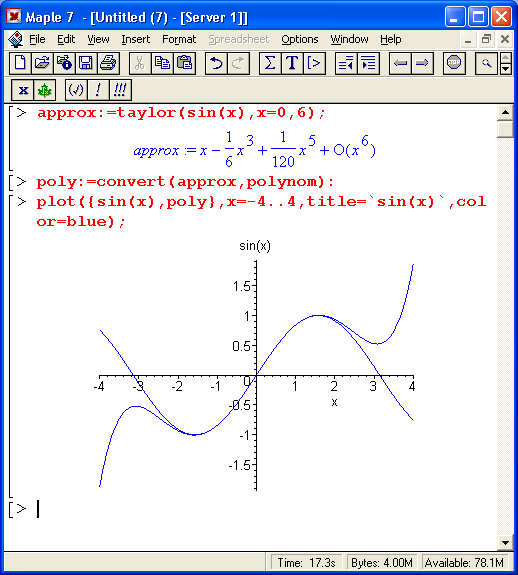
Рис. 8.8. Разложение функции sin(x) в ряд Маклорена 6-го порядка и построение ее графика
Это хороший пример визуализации результатов математических вычислений – здесь наглядно видно, что при малых значениях х график ряда практически повторяет разлагаемую функцию, но затем начинает сильно от нее отходить.
Обратите внимание, несмотря на то что мы задали шестой порядок ряда, последний член имеет только пятый порядок. Это связано со спецификой данного разложения – в нем просто отсутствуют члены четного порядка. Можно буквально в считанные секунды попробовать изменить число членов ряда или диапазон изменения переменной х, что и показано на рис. 8.9 (вторая часть документа). При этом легко убедиться в том, что при больших х поведение ряда не имеет ничего общего с поведением разлагаемой в ряд функции, в частности нет и намека на периодичность разложения, которая присуща тригонометрической функции sin(x).
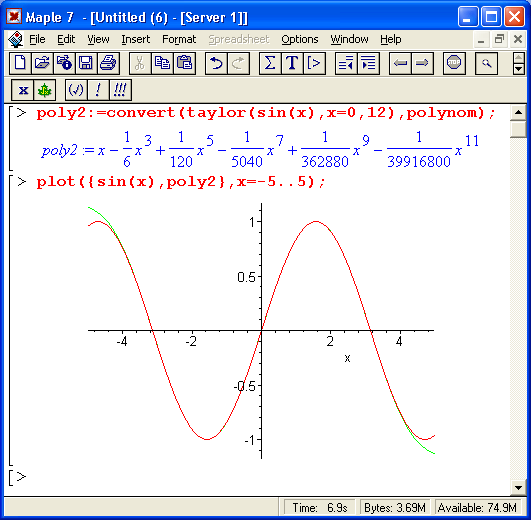
Рис. 8.9. Разложение функции sin(x) в ряд Маклорена 12-го порядка и построение ее графика
