Решение уравнений и неравенств
На рис. 8.11 показан более сложный случай решения нелинейного уравнения вида f1(x)=f2(x), где f1(х) = sin(x) и f2(x) = cos(x) -1. Решение дано в графическом виде и в аналитическом для двух случаев – нахождения главных значений корней и нахождения всех корней.
В решениях встречаются переменные _В1~ и _Z1~, означающие ряд натуральных чисел. Благодаря этому через них можно представить периодически повторяющиеся решения.
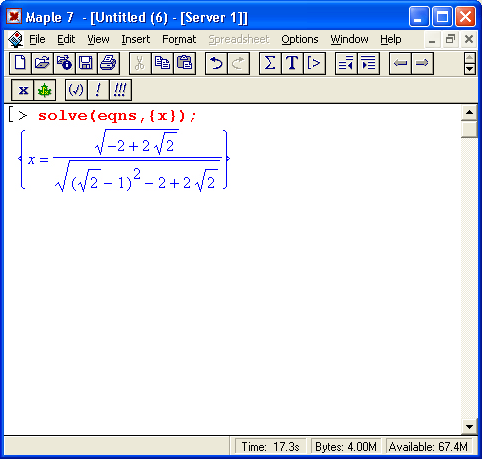
Примеры решения уравнений с обратными тригонометрическими функциями показаны ниже:
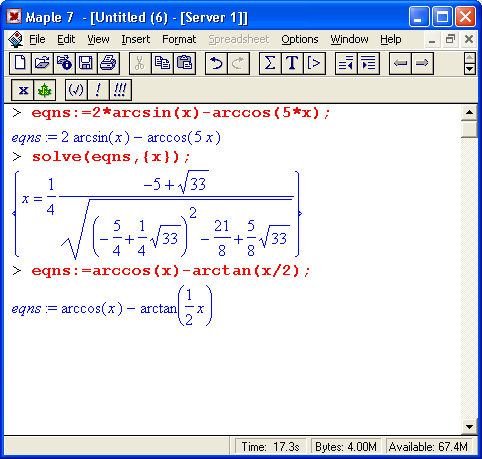
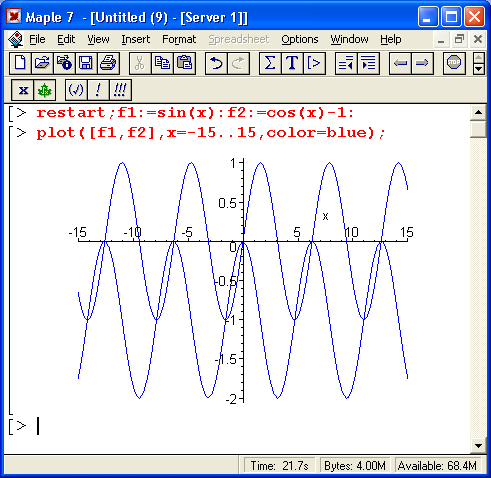
Рис. 8.11. Пример решения уравнения, имеющего периодические решения