Решение уравнений и неравенств
Основная функция solve
Решение линейных и нелинейных уравнений и неравенств – еще одна важная область математического анализа. Maple 7 имеет мощные средства для такого решения. Так, для решения линейных и нелинейных уравнений в аналитическом виде используется достаточно универсальная и гибкая функция solve(eqn, var) или solve({eqn1,eqn2,…}.{var1,var2,…}), где eqn – уравнение, содержащее функцию ряда переменных, var – переменная, по которой ищется решение, Если при записи eqn не используются знак равенства или знаки отношения, считается, что solve ищет корни уравнения eqn=0.
Характер решений можно изменить с помощью глобальных переменных:
- _SolutionsMayBeLost – при значении true дает решение, которое при обычном применении функции solve возвращает значения NULL;
- _MaxSols – задает максимальное число решений;
- _EnvAll Solutions – при значении true задает выдачу всех решений.
В решениях могут встречаться следующие обозначения:
- _NN – указывает на неотрицательные решения;
- _В – указывает на решения в бинарной форме;
- _Z – указывает на то, что решение содержит целые числа;
- %N – при текстовом формате вывода задает общие члены решения и обеспечивает более компактную форму его представления.
В форме solve[subtopic] возможны параметры subtopic функции solve следующих типов:
floats functions identity ineq linear radical scalar series system
При решении систем уравнений они и список переменных задаются как множества, то есть в фигурных скобках. При этом и результат решения получается в виде множества. Чтобы преобразовать его к обычному решению, нужно использовать функцию assign, которая обеспечивает присваивание переменным значений, взятых из множества.
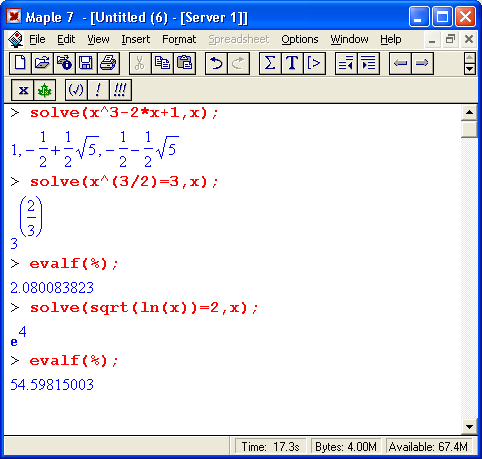
Функция solve старается дать решение в аналитическом виде. Это не означает, что ее нельзя использовать для получения корней уравнений в численном виде. Просто для этого придется использовать функции evalf или convert. Если результат решения представлен через функцию RootOf, то зачастую можно получить все корни с помощью функции all values.
Решение одиночных нелинейных уравнений
Решение одиночных нелинейных уравнений вида f(x) = 0 легко обеспечивается функций solve(f,(x),x). Это демонстрируют следующие примеры: