Вычисление сумм последовательностей
Основные формулы для вычисления сумм последовательностей
Применение систем символьной математики особенно эффективно при решении задач математического анализа. Maple 7 обладает богатейшей базой данных по формулам математического анализа и может полноценно заменять тома книг со справочными данными. При этом важно, что Maple не только "знает" многие формулы, но и может успешно использовать их при решении достаточно сложных задач в аналитическом (символьном) виде.
Начнем рассмотрение таких операций с вычисления сумм последовательностей. Вычисление суммы членов некоторой последовательности f(k) при изменении целочисленного индекса k от значения m до значения n с шагом +1, то есть выражения:
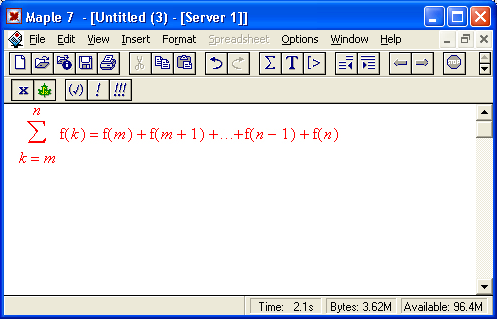
Является достаточно распространенной операцией математического анализа.
Для вычисляемой и инертной форм сумм последовательностей служат следующие функции:
sum(f.k): sum(f,k=m..n); sum(f,k=alpha): Sum(f.k); Sum(f,k=m..n); Sum(f,k=alpha);
Здесь f – функция, задающая члены суммируемого ряда, k – индекс суммирования, тип – целочисленные пределы изменения k, alpha – RootOf-выражение. Значение n может быть равно бесконечности. В этом случае для n используется обозначение ? или infinity.
Допустимо (а зачастую рекомендуется с целью исключения преждевременной оценки суммы) заключение f и k в прямые кавычки, например sum('f', 'k'=m..n). Это сделано во всех примерах справочной системы Maple 7, относящихся к функции sum. Мы, однако, отказываемся от этого в тех случаях, когда результат идентичен при заключении f и k в кавычки и без такового. Во избежание путаницы, связанной с этой тонкостью синтаксиса функции sum, рекомендуется все примеры проверять после команды restart, убирающей предыдущие определения f и k.
Последовательности с заданным числом членов
Простейшими являются суммы последовательностей с фиксированным числом членов. Ниже даны примеры применения этих функций:
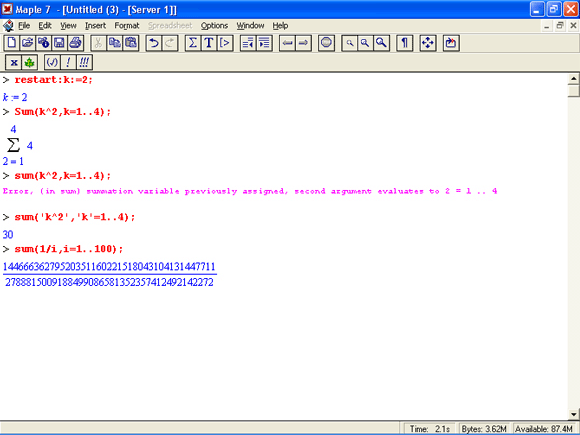
Обратите внимание, что во втором примере система отказалась от вычисления, а в третьем даже выдала сообщение об ошибке, связанной с тем, что переменной k перед вычислением сумм было присвоено численное значение 2. После заключения выражения и переменной индекса k в прямые кавычки ошибка исчезла, поскольку такая операция означает, что переменной придается неопределенное значение.
