Вычисление произведений членов последовательностей
Как и в случае вычисления сумм, вычисление произведений возможно как в численной, так и в аналитической форме – разумеется, если таковая существует.
Это показывает следующий пример:
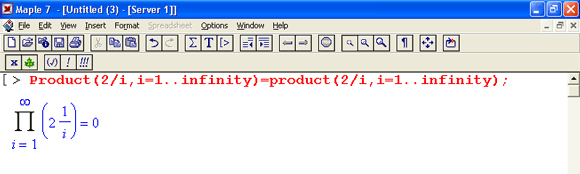
Нетрудно понять, что при i, стремящемся к бесконечности, перемножаемые члены последовательности стремятся к нулю, а потому к нулю стремится и их произведение. Вопросы доказательства подобных утверждений находятся за рамками данного учебного курса, ибо он посвящен не математике как таковой, а конкретной программе для математики – Maple 7.
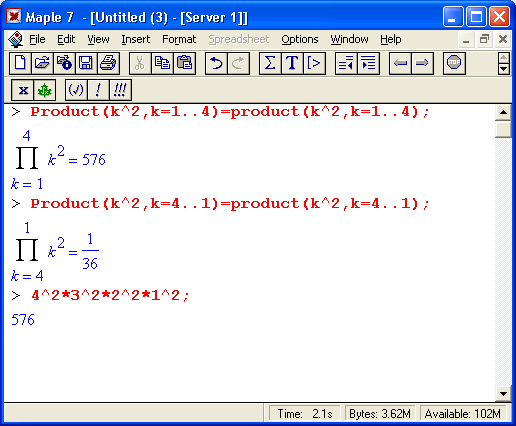
От перемены места сомножителей произведение меняется!
Хотя произведение не зависит от порядка расположения сомножителей, их перестановка в Maple 7 недопустима.
Это иллюстрируют следующие примеры:
Внимание
При вычислении произведений надо строго соблюдать прямой (нарастающий) порядок задания значений индексной переменной произведения. Нарушение этого порядка чревато грубыми ошибками.
