Вычисление сумм последовательностей
Суммы с заданным пределом
Особый класс образуют последовательности, у которых предел задается в общем виде значением переменной. Ниже представлен ряд последовательностей, у которых предел задается как 0. .n или 1. .n:
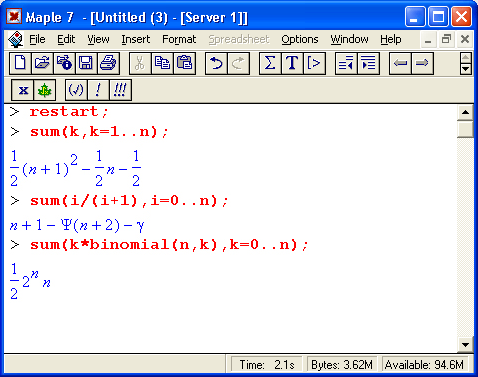
Такого рода последовательности, как видно из приведенных примеров, нередко имеют аналитические выражения для своего значения. Его вычисление намного проще, чем формирование заданной последовательности с прямым суммированием ее членов. Некоторые из таких сумм выражаются через специальные математические функции.
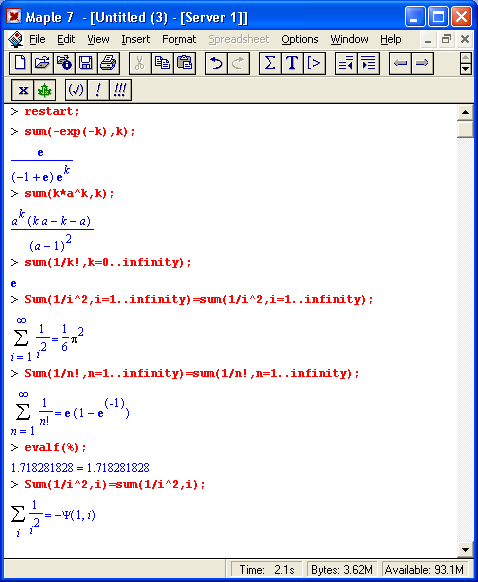
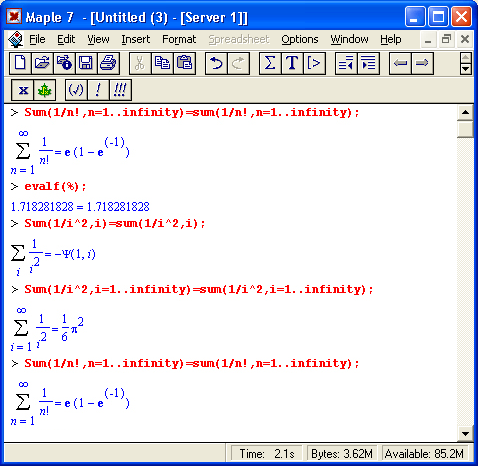
Суммы бесконечных последовательностей
Многие суммы бесконечных последовательностей сходятся к определенным численным или символьным значениям, и система Maple 7 способна их вычислять.
Это поясняют следующие примеры: