Операции с полиномами
Разложение полинома на множители
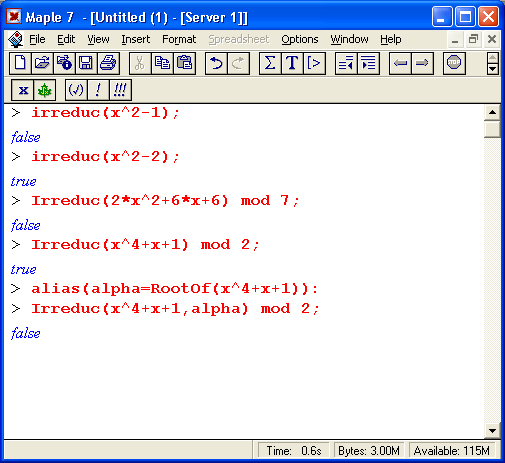
Для контроля того, имеет ли полином несокращаемые множители, может использоваться функция irredik(p) и ее вариант в инертной форме Ireduc(p.K), где К – RootOf-выражение. Ниже приведены примеры применения этих тестовых функций:
Разложение полинома по степеням
Для разложения полинома р по степеням служат инертные функции AFactor(р) и AFactors(p). Полином может быть представлен в виде зависимости от одной или нескольких переменных.
Функция Afactor(p) выполняет полную факторизацию (разложение) полинома р от нескольких переменных с коэффициентами в виде алгебраических чисел над полем комплексных чисел. При этом справедливо отношение evala(AFactor(p))=factor(p,complex). Таким образом, эта функция является, по существу, избыточной.
В случае одномерного полинома полное разложение на множители является разложением на линейные множители. Функция AFactors аналогична функции Afactor, но создает структуру данных формы [u,[[f[l],e[l]],….[f[n],e[n]]]] так, что p=u*f[l]xe[l]*…*f[n]^e[n], где каждый f[i] – неприводимый полином.
Ниже даны примеры применения функции Afactor:
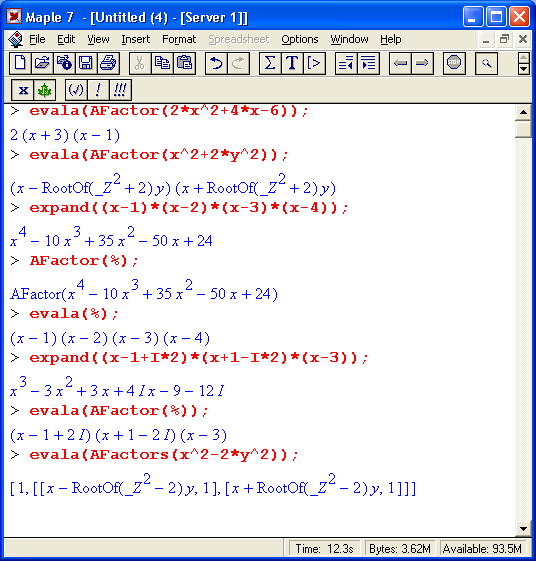
Нетрудно заметить, что разложение полинома на множители позволяет оценить наличие у него корней. Однако для этого удобнее воспользоваться специальными функциями, рассмотренными ниже.
