Пример анализа сложной функции
Ниже мы рассмотрим типичный анализ достаточно "сложной" функции, имеющей в интересующем нас интервале изменения аргумента х от -4 до 4, нули, максимумы и минимумы. Определение функции f(x), ее графики и график производной dF(x)/dx даны на рис. 9.2. Этот рисунок является началом полного документа, описываемого далее.
Функция F(x) на первый взгляд имеет не совсем обычное поведение вблизи начала координат (точки с х =у = 0). Для выяснения такого поведения разумно построить график функции при малых х и у. Он также представлен на рис. 9.2 (нижний график) и наглядно показывает, что экстремум вблизи точки (0, 0) является обычным минимумом, немного смещенным вниз и влево от начала координат. Теперь перейдем к анализу функции F(x). Для поиска нулей функции (точек пересечения оси х) удобно использовать функцию fsolve, поскольку она позволяет задавать область изменениях, внутри которой находится корень. Как видно из приведенных ниже примеров, анализ корней F(x) не вызвал никаких трудностей, и все корни были уточнены сразу.
Поиск нулей функции:
> fsolve(F(x),x,-2…-1): -1.462069476 > fsolve(F(x),x,-0.01..0.01); 0. > fsolve(F(x).x.-0.05..0); -0.02566109292 > fsolve(F(x),x,1..2); 1.710986355 > fsolve(F(x),x,2.5..3): 2.714104921
Нетрудно заметить, что функция имеет два очень близких (но различных) корня прих, близких к нулю.
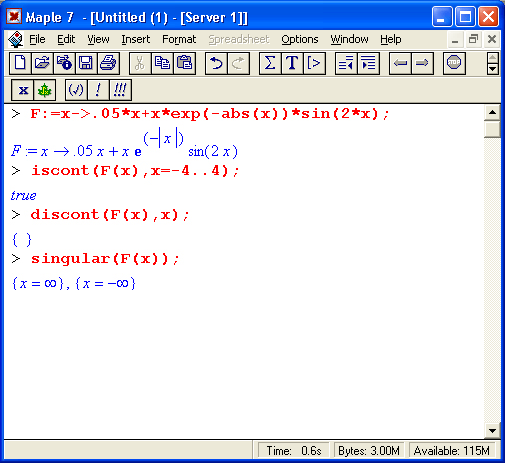
Анализ функции на непрерывность, наличие ее нарушений и сингулярных точек реализуется следующим образом.
Анализ функции на непрерывность, наличие ее нарушений и наличие сингулярных точек: