Анализ функций
Приведем подобные примеры и для функции поиска максимума – maximize:
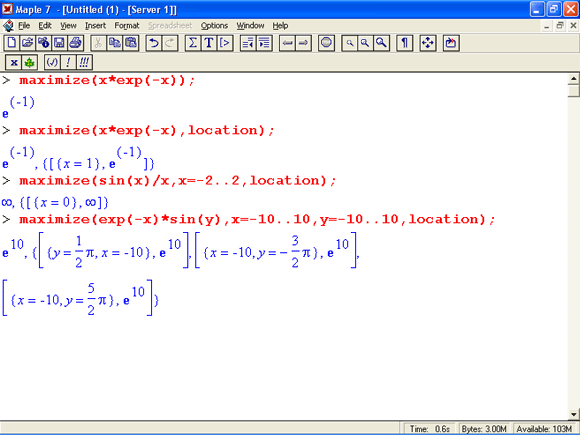
Обратите внимание на то, что в предпоследнем примере Maple 7 явно "оскандалилась" и вместо максимума функции sin(x)/x, равного 1 при х=0, выдал результат в виде бесконечности. Другими словами, система обнаружила, что в данном случае ей незнакомо понятие предела sin(x)/x при х › 0. Эта ситуация кажется более чем странной, если учесть, что в этом примере Maple 6 давал правильный результат.
Применим функцию minimize для поиска минимума функции Розенброка. Рисунок 9.1 показывает, что minimize прекрасно справляется с данной задачей. На рис. 9.1 представлено также построение функции Розенброка, хорошо иллюстрирующее ее особенности.
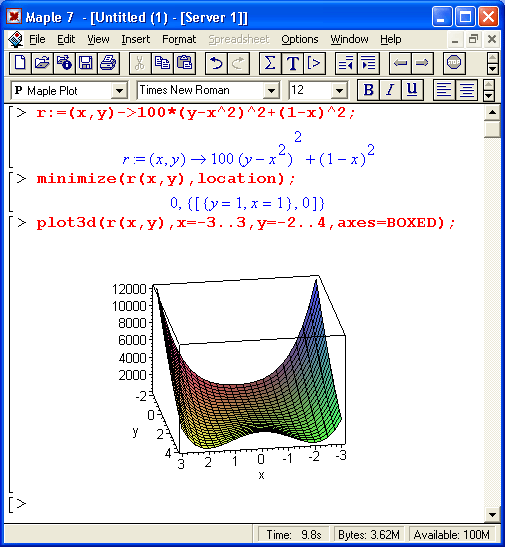
Рис. 9.1. Поиск минимума функции Розенброка и построение ее графика
Трудность поиска минимума функции Розенброка связана с ее характерными особенностями. Из рис. 9.1 видно, что эта функция представляет собой поверхность типа "глубокого оврага с почти плоским дном", в котором и расположена точка минимума. Такая особенность этой функции существенно затрудняет поиск минимума. То, что система Maple 7 справляется с данной тестовой функцией, вовсе не означает, что трудности в поиске минимума или максимума других функций остаются позади.
