Анализ функций
Для проверки оптимизационных алгоритмов существует ряд тестовых функций. Одна из таких функций – функция двух переменных Розенброка. В представленном ниже примере она задана как rf(x.y):
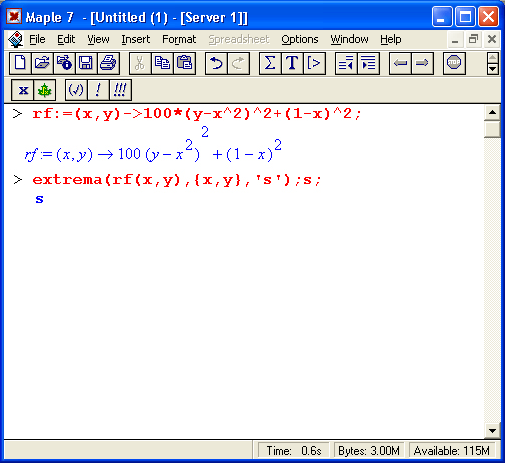
Как нетрудно заметить, минимум этой функции при значениях х =у = 1, равный 0, функцией extrema не обнаружен. Однако это не недостаток данной функции, а просто неудачное ее применение. Функция Розенброка имеет минимум значения, и для его обнаружения надо использовать функцию minimize, описанную ниже.
Примечание
Функция extrema дает неплохие результаты при поиске экстремумов простых аналитических функций, не имеющих особенностей. Однако при анализе сложных функций, содержащих функции со сравнением аргумента (например, abs(x), signum(x) и др.), функция extrema часто отказывается работать и просто повторяет запись обращения к ней.
Поиск минимумов и максимумов аналитических функций
Часто нужно найти минимум или максимум заданной функции. Для поиска минимумов и максимумов выражений (функций) ехрr служат функции стандартной библиотеки:
minimize(expr, optl, opt2,… .optn) maximize(expr, optl .opt2…. .optn)
Эти функции могут разыскивать максимумы и минимумы для функций как одной, так и нескольких переменных. С помощью опций opt1, opt2,…, optn можно указывать дополнительные данные для поиска. Например, параметр `infinity` означает, что поиск минимума или максимума выполняется по всей числовой оси, а параметр location (или locatiorrtrue) дает расширенный вывод результатов поиска – выдается не только значение минимума (или максимума), но и значения переменных в этой точке.
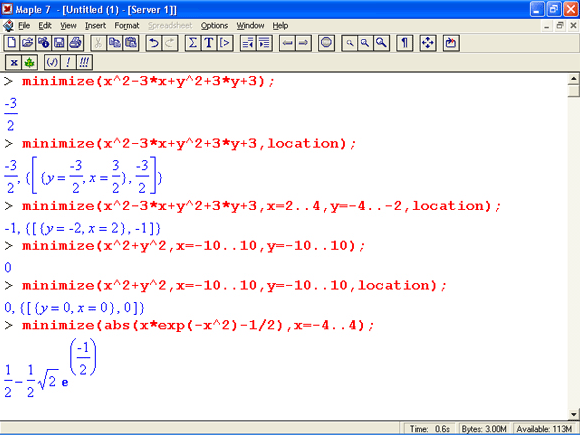
Примеры применения функции minimize приведены ниже: